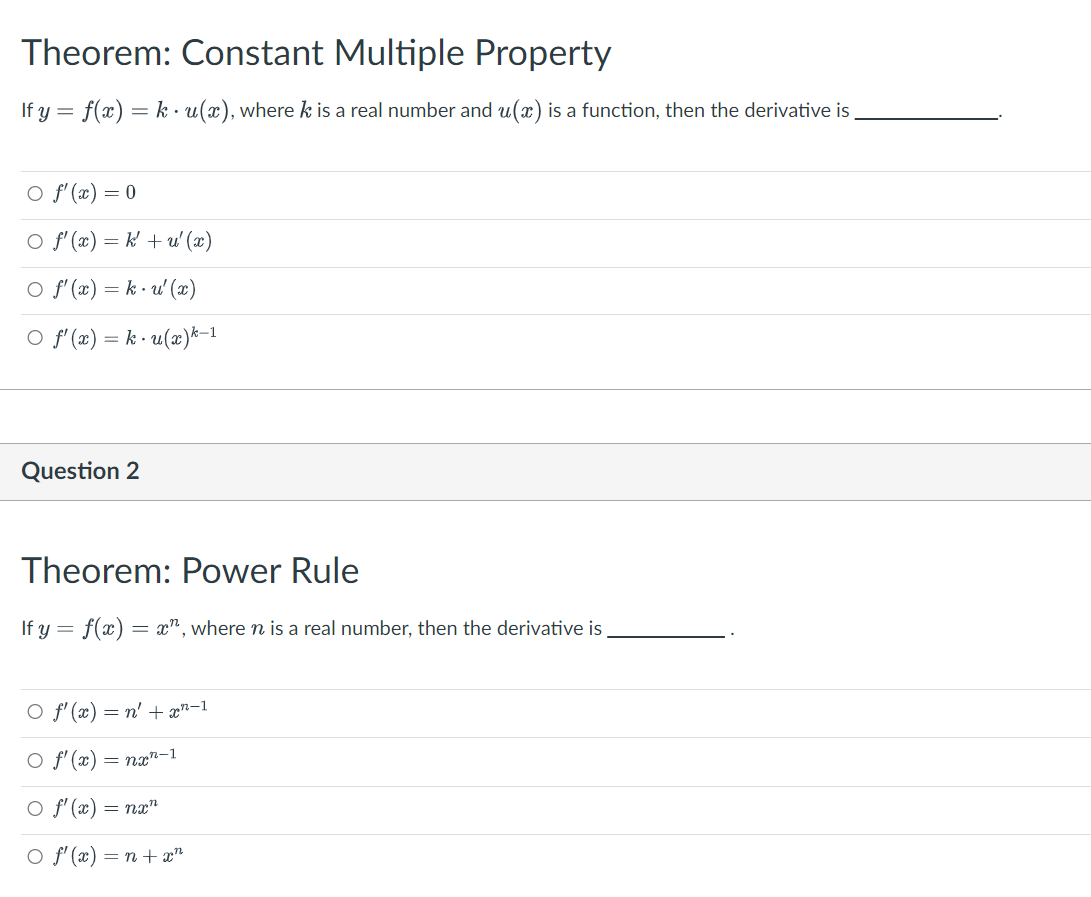
Theorem: Constant Multiple Property If y = f(x) = k u(x), where k is a real number and u(x) is a function, then the derivative is. f'(x) = 0 O f'(x) = k' + u' (x) f'(x) = k u' (x) O f'(x) = k u(x)k-1 Question 2 Theorem: Power Rule If y = f(x) = x, where n is a real number, then the derivative is f'(x) = n' + x-1 f'(x) n-1 f'(x) f'(x) = n+xn Question 3 If y = f(x), then f'(x), y', d, and f(x) all represent the [Select] off at x.