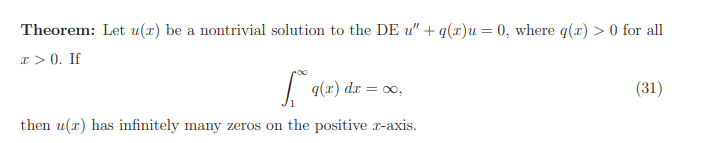
Theorem: Suppose that g(r) 0 for all r >0. If 30 q(x) dx = 00, (31) then u(r) has infinitely many zeros on the positive r-axis.cy'' oy Fay=0, x>0 (i) What is the normal form of the DE? (ii) For what values of v, the solutions of the DE will be oscillatory? (have infinitely many zeros) (iii) For what values of , the solutions of the DE will not be oscillatory? (have at most one zero)