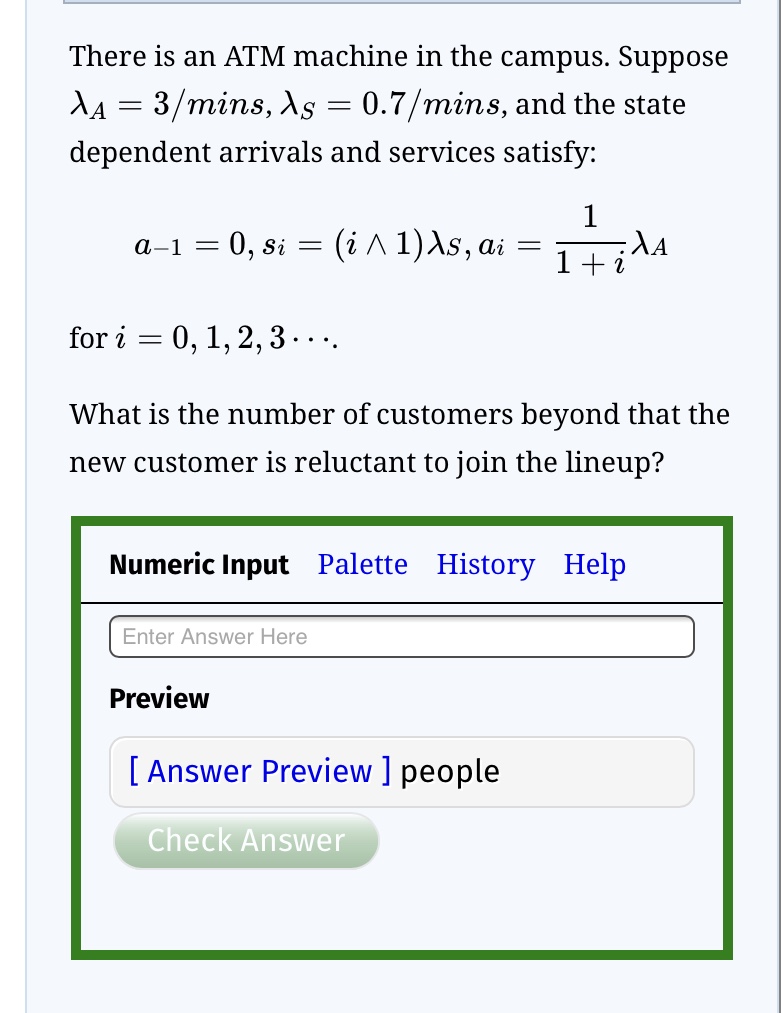
Question: There is an ATM machine in the campus. Supposelambda_{A}=3/mins ??A ??=3/mins,lambda_{S}=0.7/mins ??S ??=0.7/mins, and the state dependent arrivals and services satisfy: displaystyle a_{-1}=0, s_{i}=(i wedge
There is an ATM machine in the campus. Suppose\lambda_{A}=3/mins
??A
??=3/mins,\lambda_{S}=0.7/mins
??S
??=0.7/mins, and the state dependent arrivals and services satisfy:
\displaystyle a_{-1}=0, s_{i}=(i \wedge 1)\lambda_{S}, a_{i}=\frac{1}{1+i}\lambda_{A}
a??1
??=0,s?i
??=(i?1)??S
??,a?i
??=?1+i
?
?1
????A
??fori=0, 1, 2, 3 \cdots
i=0,1,2,3?.
What is the number of customers beyond that the new customer is reluctant to join the lineup?
There is an ATM machine in the campus. Suppose AA = 3/ms'ns, A3 = 0.7/ms'ns, and the state dependent arrivals and services satisfy: 1 (11 =0,sr = (3A 1)/\\S,or = 1+Z./\\A fori=0,1,2,3~-. What is the number of customers beyond that the new customer is reluctant to join the lineup? Numeric Input Palette History Help Enter Answer Here Preview [Answer Preview] people
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


