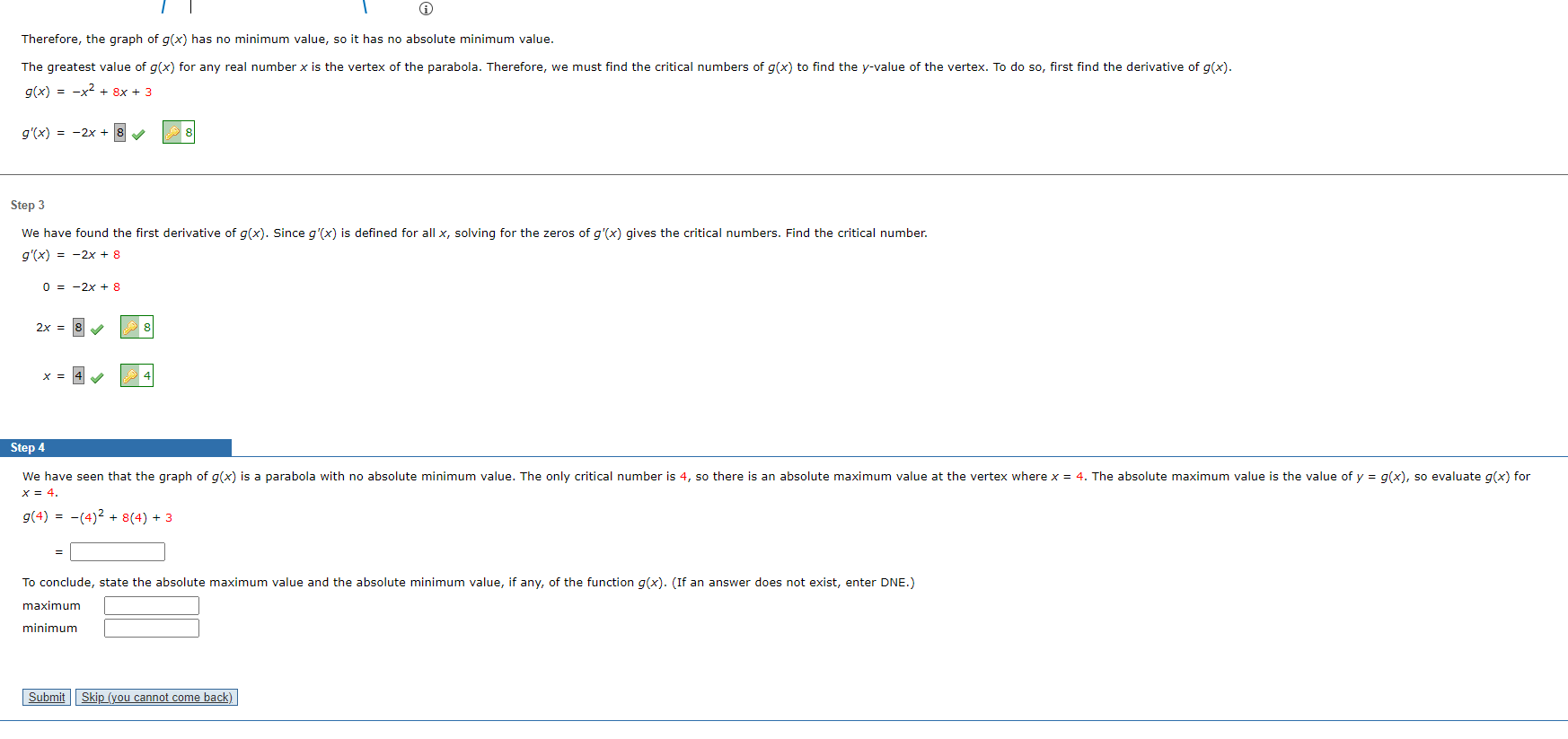
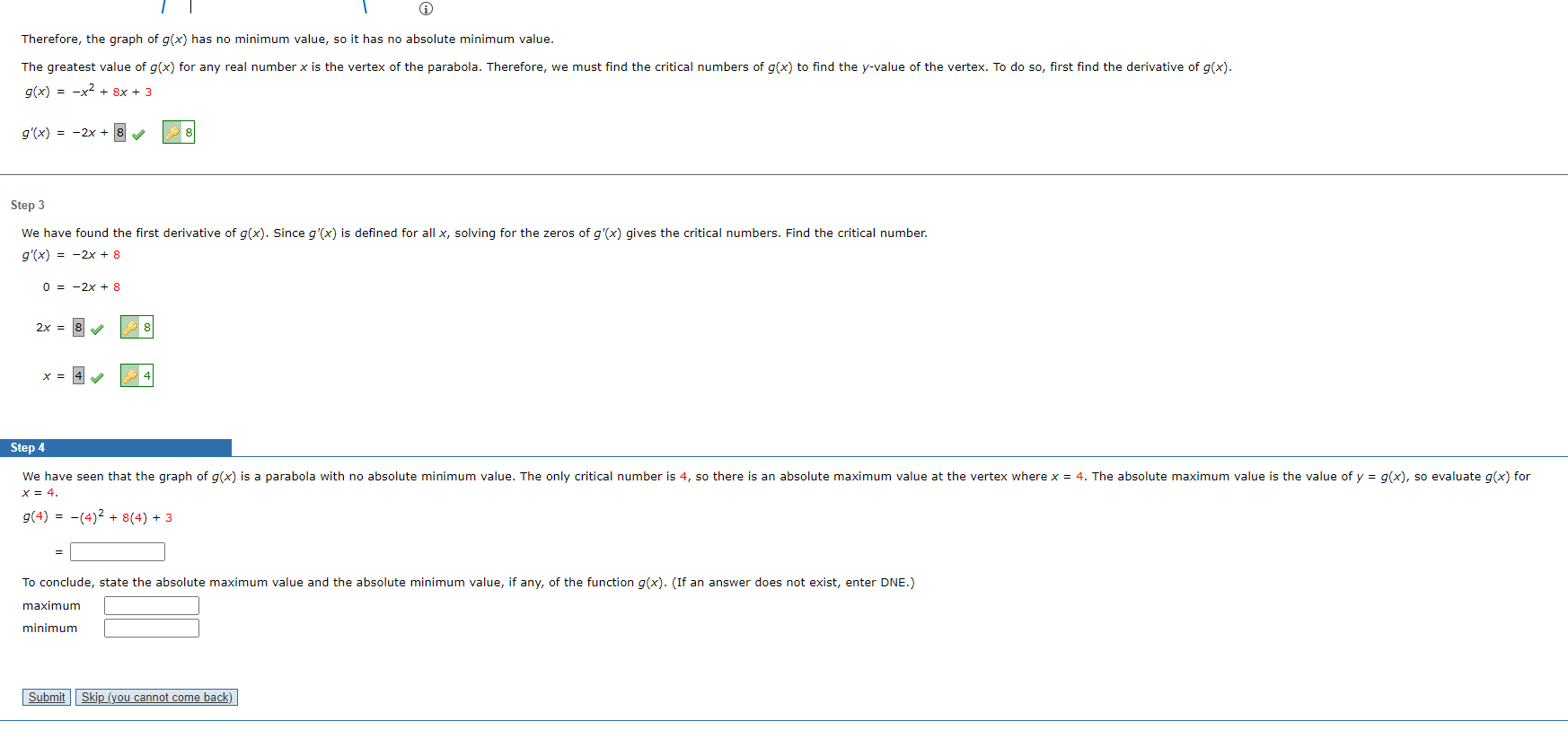
Therefore, the graph of g(x) has no minimum value, so it has no absolute minimum value. The greatest value of g(x) for any real number x is the vertex of the parabola. Therefore, we must find the critical numbers of g(x) to find the y-value of the vertex. To do so, first find the derivative of g(x). g(x) = -x2 + 8x+ 3 g ' ( x ) = - 2x + 8 0 8 Step 3 We have found the first derivative of g(x). Since g'(x) is defined for all x, solving for the zeros of g'(x) gives the critical numbers. Find the critical number. g'(x) = -2x + 8 0 = -2x + 8 2x = 8 0 * = 40 $ 4 Step 4 We have seen that the graph of g(x) is a parabola with no absolute minimum value. The only critical number is 4, so there is an absolute maximum value at the vertex where x = 4. The absolute maximum value is the value of y = g(x), so evaluate g(x) for X = 4. 9 (4 ) = -(4)2 + 8(4) + 3 To conclude, state the absolute maximum value and the absolute minimum value, if any, of the function g(x). (If an answer does not exist, enter DNE.) maximum minimum Submit Skip (you cannot come back)