This assignment i have is aimed to teach us to learn the basics of how google (search engine) works. I am pretty lost on how to approach this. any help would be great. computations are good, but explanation is better. Thanks in advance.

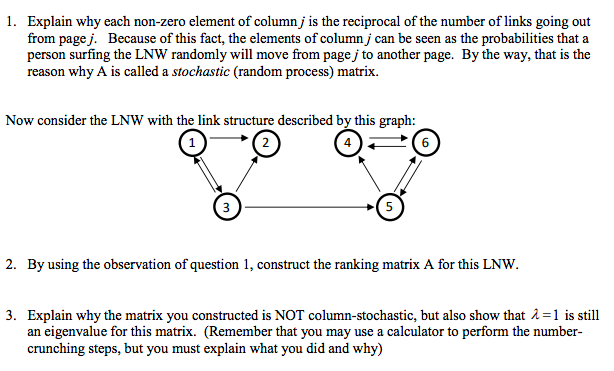
Let's consider a LNW consisting of 4 pages that include links as shown here: In this small web, page 1 includes three links, sending you to each of the other pages. On the other hand, page 2 includes references to 3 and 4 only, while page 3 only links to 1. (Quickly check where page 4 links to). At this point we notice that page 1 is not very discriminating, as it links to everywhere else, but it may be a reliable or even important page. On the other hand, page 3 is very selective, so it probably links only to important pages, but it may not be important or reliable itself. In order to provide a balance between these two competing criteria, we start by defining the rank of a page through the following expression: Rank (i)- ? Rank() So, for instance, to express the rank of page1 we use pages 3 and 4 only, since they are the only ones that link to it, and we get Rank(u)- Ran(3)Rank (4) By repeating this for all four pages and slimming down the notation, we end up with a linear system: 1/3 0 00 3 2 If we call the above matrix the ranking matrix and denote it by A, we can notice two important things: The elements of each column of A are all non-negative, not all0, and add up to1. Such a matrix The vector r consisting of the four ranks is an eigenvector for A with eigenvalue 1. We call it is called a column-stochastic matrix the ranking vector. Let's consider a LNW consisting of 4 pages that include links as shown here: In this small web, page 1 includes three links, sending you to each of the other pages. On the other hand, page 2 includes references to 3 and 4 only, while page 3 only links to 1. (Quickly check where page 4 links to). At this point we notice that page 1 is not very discriminating, as it links to everywhere else, but it may be a reliable or even important page. On the other hand, page 3 is very selective, so it probably links only to important pages, but it may not be important or reliable itself. In order to provide a balance between these two competing criteria, we start by defining the rank of a page through the following expression: Rank (i)- ? Rank() So, for instance, to express the rank of page1 we use pages 3 and 4 only, since they are the only ones that link to it, and we get Rank(u)- Ran(3)Rank (4) By repeating this for all four pages and slimming down the notation, we end up with a linear system: 1/3 0 00 3 2 If we call the above matrix the ranking matrix and denote it by A, we can notice two important things: The elements of each column of A are all non-negative, not all0, and add up to1. Such a matrix The vector r consisting of the four ranks is an eigenvector for A with eigenvalue 1. We call it is called a column-stochastic matrix the ranking vector