This class QuickFindUF2 is based on QuickFindUF from our textbook. In particular, we still have the following "quick find" feature:

* For each item p, id[p] is its leader (component identifier), so we can compute find(p)==id[p] in O(1) time. However, we added the following new features:

* We add a size[] array. For each item p, the size of its component is size[id[p]]. Method size(p) returns this. * We add a next[] array. For each component, we keep its items, including the leader, in a circular linked list. For each item p, the next item in its list is next[p]. * Whenever we union two distinct components, we traverse the list of the smaller component. For each item k in that list, we modify id[k] to equal the leader of the larger component. Then we link the two circular lists into one.

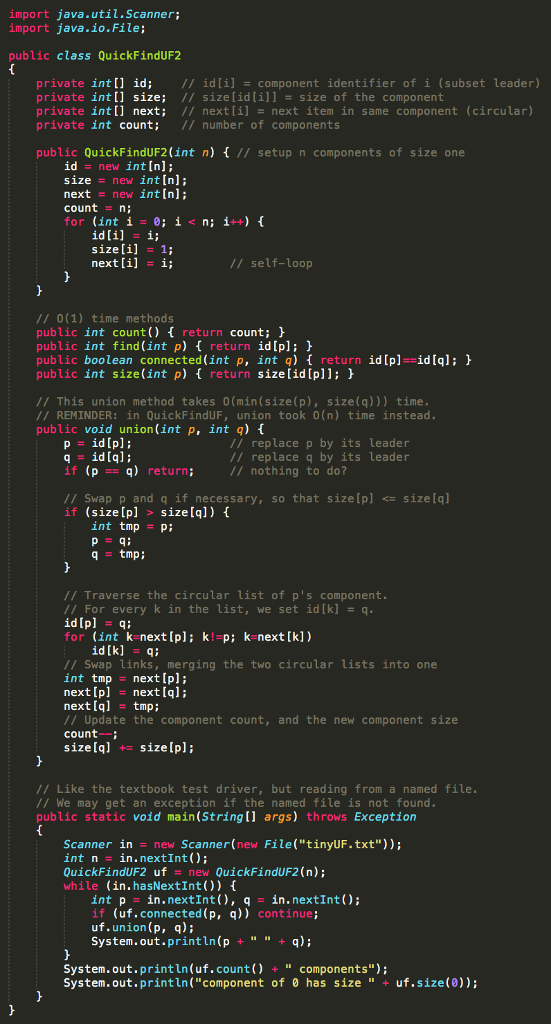
Problem 1. Read share/writ1/QuickFindUF2.java. This is a more efficient variation of the textbook class QuickFindUF. In this version, we keep a circular linked list of all the items in each component. When we join two components, we traverse the smaller list, resetting the id of each item to that of the larger component.

1(a). The textbook UF datastructures use N + O(1) or 2N + O(1) words of memory, for a structure of size N. (A word is enough memory to store one int, and the +O(1) term includes some JVM overhead to keep track of the object and array.) How much space is used by a QuickFindUF22 of size N?

1(b). Fix some item i. Argue that whenever a union operation modifies id[i], the size of is component at least doubles. Conclude that id[i] is modified O(lg N) times.

1(c). Suppose we construct a QuickFindUF2 structure of size N, and then we do some sequence of M operations (unions and finds) on it. Argue that the total running time is O(M + N lg N). Remark: Your answer here should use the previous part, and the idea is to charge the work of traversing a list to the items in that list. You only need a few sentences.

import java.util.Scanner; import java.io.File; public class QuickFindUF2 private int[] id;I/ id[i] component identifier of i (subset leader) private int[] size; // size [id[]] = size of the component private int[] next; // next[i]-next item in same component (circular) private int count; // number of components public QuickFindUF2 (int n)t//setup n components of size one id new int [n]; size new int [n]; next new intInl count n; for (int i 0; i size[q]) int tmpp; // Traverse the circular list of p's component. IFor every k in the list, we set id[k]q for (int k-nextIpl: k!-p: k-next[k]) // Swap links, merging the two circular lists into one int tmp next[pl: next Ipl next[q]; next[q] tmp; // Update the component count, and the new component size count-- size[q] +size[pl: // Like the textbook test driver, but reading from a named file // We may get an exception if the named file is not found public static void main(String[] args) throws Exception Scanner in new Scanner(new File("tinyUF. txt")); int n in.nextInt); QuickFindUF2 ufnew QuickFindUF2 (n); while (in.hasNextInt()) int p in.nextInt), q in.nextInt if (uf.connected (p, q)) continue; uf.union (p, q); System.out.println(p "q)i System.out.println(uf.count) " components"); System.out.println("component of 0 has size "+ uf.size(0)); import java.util.Scanner; import java.io.File; public class QuickFindUF2 private int[] id;I/ id[i] component identifier of i (subset leader) private int[] size; // size [id[]] = size of the component private int[] next; // next[i]-next item in same component (circular) private int count; // number of components public QuickFindUF2 (int n)t//setup n components of size one id new int [n]; size new int [n]; next new intInl count n; for (int i 0; i size[q]) int tmpp; // Traverse the circular list of p's component. IFor every k in the list, we set id[k]q for (int k-nextIpl: k!-p: k-next[k]) // Swap links, merging the two circular lists into one int tmp next[pl: next Ipl next[q]; next[q] tmp; // Update the component count, and the new component size count-- size[q] +size[pl: // Like the textbook test driver, but reading from a named file // We may get an exception if the named file is not found public static void main(String[] args) throws Exception Scanner in new Scanner(new File("tinyUF. txt")); int n in.nextInt); QuickFindUF2 ufnew QuickFindUF2 (n); while (in.hasNextInt()) int p in.nextInt), q in.nextInt if (uf.connected (p, q)) continue; uf.union (p, q); System.out.println(p "q)i System.out.println(uf.count) " components"); System.out.println("component of 0 has size "+ uf.size(0))