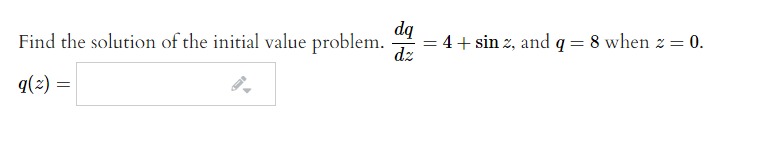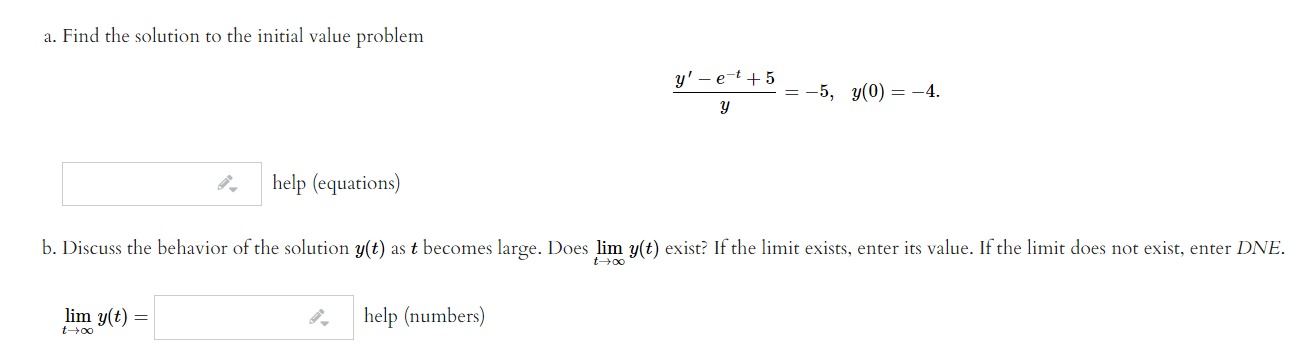This comes from the textbook Differential Equations and Linear Algebra 4th edition.

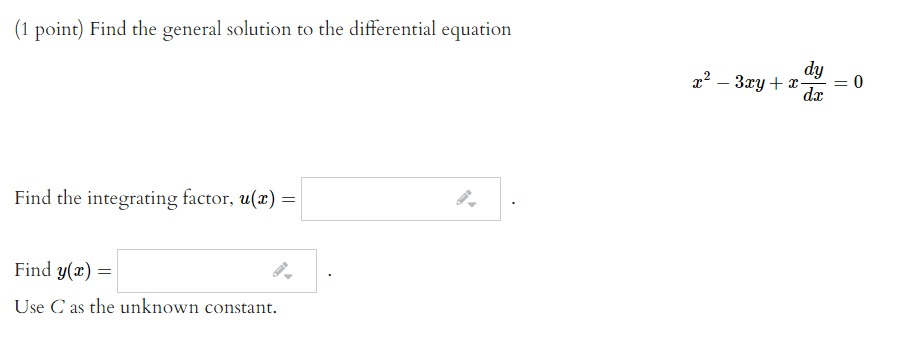
Find the solution of the initial value problem. dq dz = 4 + sin z, and q = 8 when z = 0. q(2) =(3) Consider the differential equation :3y=0. Find a general solution to this differential equation that has the form 3; = 02". y = .91, Find a second solution y : Cm" that might not be a general solution and which may have a different value of 1:. than your rst solution. y = .91, (b) If the solution additionally satises y = 25 when a: = 5, what is the solution? y = .91, Find the general solution to (t2 + 4)y' + 21:3; 2 2032 + 4). Enter your answer 3.5 y = - . . . Use 0 to denote the arbitrary constant in your answer- 59', help {equations} a. Find the solution to the initial value problem yr 78: + 5 = ,5, gm) = *4. l .f' help (equations) b. Discuss the behavior at the solution t) as it becomes large. Does Kim Mt} exist? If the limit exists, enter its value. If the limit does not exist, enter DNE. tMx: 130 Silt) = i, help (numbers) Consider the intial value problem a. Find a nonzero solution to the associated homogeneous differential equation. 1; =' .92. J help (formulas) h. Find a particular solution to the nonhomogeneous differential equation. y =' .4\Find the general solution to ihlilg + r = 2:31. Enter your answer as r : . . . . Use 0 to denote the arbitrary constant in your answer. ,9: help {equations} {1 point]I Find the general solution to the differential equation Find the integrating factor, 11(2) : #7., Find mm) = ; Use C a5 the unknown constant. (1 point) Solve the initial value problem dy dt - y = 7et + 10et with y(0) = 4. y =[:1 point) Find the general solution, y(t), which solves the Problem below, by the method of integrating factors. '13) 2 5t 2: dt +9 Find the integrating factor, u[t] = l #1. l , and then nd y{t) 2! f, . {use C as the unkown constant.) (1 point) Solve the following initial value problem: dy d+ + 3y = 7t with y(1) = 2. Find the integrating factor, u(t) = and then find y(t) =