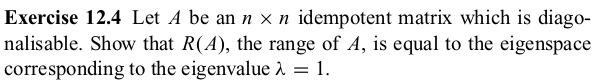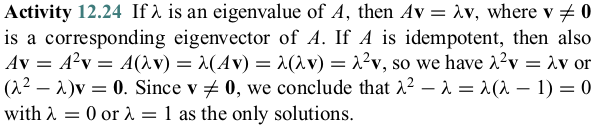This is a Linear Algebra question.

Both the QUESTION and SOLUTION are shown

My question is regarding the SOLUTION shown below

1. How was ?a1?v1?+a2?v2?+?+ai?vi?? obtained from the previous step, underlined in BLUE

Please explain clearly showing each step as thoroughly as possible.

If you are using hand-written notes, then please ensure they are tidy and legible as untidy written notes are difficult to interpret.

Alternatively use LaTeX.

QUESTION

Exercise 12.4 Let A be an n x n idempotent matrix which is diago- nalisable. Show that R(A), the range of A, is equal to the eigenspace corresponding to the eigenvalue ^ = 1.Activity 12.24 If ^ is an eigenvalue of A, then Av = Av, where v # 0 is a corresponding eigenvector of A. If A is idempotent, then also Av = A'v = A()V) = M(AV) = )(.v) = >'v, so we have A v = Av or ()2 - 2)v = 0. Since v # 0, we conclude that ) - 2 = 2(2 - 1) = 0 with % = 0 or > = 1 as the only solutions.Exercise 12.4 You have already shown in Activity 12.24 that the only eigenvalues of an idempotent matrix are A = 1 and 2 = 0. Since A can be diagonalised, there is an invertible matrix P and a diago- nal matrix D = diag(1, . . ., 1, 0, ..., 0) such that P-AP = D. Let V1, V2, . . ., Vn denote the column vectors of P with v1, ..., v; being eigenvectors for 2 = 1 and vit1, ..., Vn eigenvectors for A = 0. Then B = (V1, V2, . .., Vn) is a basis of R" and (v1, . . ., v;) is a basis of the eigenspace, E(1), for eigenvalue ) = 1. If y E R(A), then y = Ax for some x E R". Now, x can be writ- ten as a unique linear combination x = a V1 + a2v2 + . . . + an Vn. We therefore have y = Ax = A(a| V1 + a2V2 + . . . + anVn) = al AV1 + a2 Av2 + . . . + an AVn = al VI + a2v2 + .. . + diVi since Av; = v; for j = 1, . .., i and Av; = 0 for j = i + 1, . . .,n. Therefore, y E E(1), so R(A) C E(1). Now let y E E(1). Then y e R" and Ay = y, so y E R(A). This completes the proof