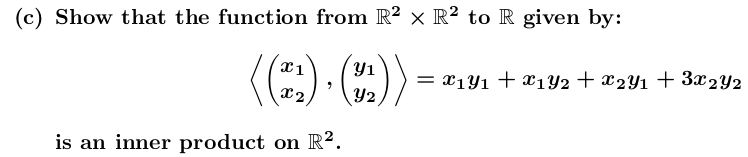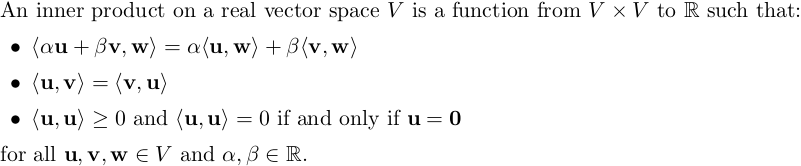This is a Linear Algebra question regarding inner products.

Both the QUESTION and SOLUTION are shown below.

How is:

?(u1?+u2?)2+2u22??0? UNDERLINED BLUE obtained from ?u12?+2u1?u2?+3u22?? (UNDERLINED RED) in the SOLUTION shown.

Please explain clearly showing each step as thoroughly as possible.

If you are using hand-written notes, then please ensure they are tidy and legible as untidy written notes are difficult to interpret.

Alternatively use LaTeX.

QUESTION

c Show that the function from R2 X R2 to R iven b : g 3' = 113131 + 113132 + 113291 + 3113292 2 292 is an inner product an R2. An inner product on a real vector space V is a function from V x V to R such that: I (on | aw) = o:(u?w) | aw) - (unr) = (mu) a (u,u} 3 0 and (u,u} : 0 if and onlj,r if u: [I for all u,v,w E V and [2,3 E R. (c) To show that the function from R2 x R2 to R given by: is an inner product on R', we note the following. . For any u, v, w E R' and o, B E R we have: ( a (13 ) + 13 ( 13 ) . ( 103 ) > = au1 + Bui ) Qu2 + BU2) = (au + Bul)wi + (au, + Bul)w2 + (au2 + Bv2)wi + 3(ouz + Bv2)w2 = o (uw1 + ulw2 + u2w1 + 3u2w2) + B(viw1 + viw2 + vow1 + 302w2) = a ((i). ( 13) ) + 8 ( (05). (203 ) > . For any u, v E R' we have: . For any u E R' we have: ( ( 213) . ( 12 ) ) = 13 + 1, us + using + 31/? = 13 + 20ju2 + 317 = (11 + 12)? + 213 20. Moreover, if we have: us = 0 then we have ( ( 13 ) . ( 13 ) ) = 13 + 201 12 + 313 = 0 as u1 = u2 = 0 and, if we have: ( ( 23 ) . ( " ) ) = 0 then we have ( uz + 12 )? which, as the sum of two squares, means that uj + u2 = 0 and u2 = 0, i.e. we have u2 = 0 and u1 = -u2 = 0 so that (u1, u2) = 0. Therefore, as required, the given function satisfies the definition of an inner product on R2