Question: This is a MATLAB Ccode Problem 20 Solution Six MATLAB Grade Mal Mpotong bao ASC210 Project 2 - www mounts/3033821021/problem/345710 problem solutionsew Brian Kouse Mpoki

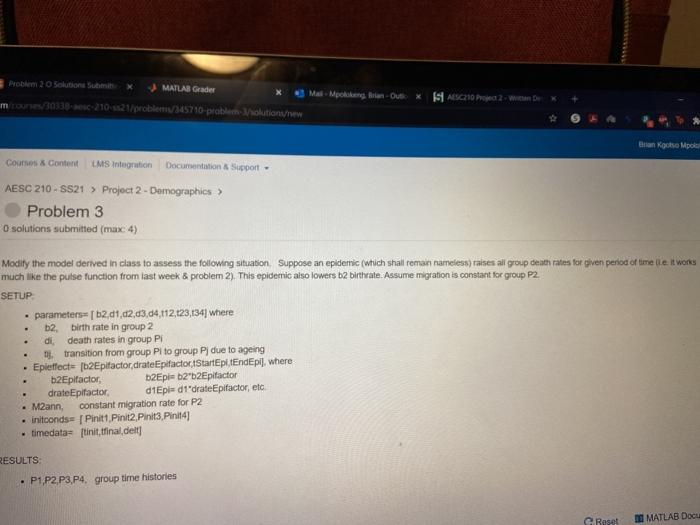
This is a MATLAB Ccode This is a MATLAB Ccode Problem 20 Solution Six MATLAB Grade

Problem 20 Solution Six MATLAB Grade Mal Mpotong bao ASC210 Project 2 - www mounts/3033821021/problem/345710 problem solutionsew Brian Kouse Mpoki Course Content LMS Integration Documentation & Support AESC 210-SS21 > Project 2-Demographics > Problem 3 O solutions submitted (max 4) - . Modity the model derived in class to assess the following situation. Suppose an epideric (which shall remain nameless) raises all group death rates for giver period of time lle tworks much like the pulse function from last week & problem 2). This epidemic also lowers b2 birtheate. Assume migration is constant for group P2. SETUP parameters= [62.01,12,13,04,112,123,134] where b2 birth rate in group 2 di death rates in group PI o transition from group Pi to group PJ due to ageing Epleffect [b2Epifactor,drateEpifactor StartEp. tEndEpil, where b2Epifactor D2Epie b2b2Epifactor drateEpifactor d1 Epi=d1"drateEpifactor, etc Mann, constant migration rate for P2 Initconds [Pinit1 Pinit2. Pinit3 Pinit4) . timedata= [tinit,tfinal delt . RESULTS P1,P2 P3, P4, group time histories e Reset MATLAB Docu Grader Mail - Mpolokeng, Brian - Outlo > =1300742 ses described below using the following differentia nations has also been provided for reference. dP1/dt = BR*P2 -d1*P1 -t12*P1 dP2/dt = t12*P1 -d2*P2 -t23*P2 dP3/dt = t23*P2 -d3*P3 -t34*P3 dP4/dt = t34*P3 -d4*P4 igure 1: Differential Equations for Modeling 4 linked population Problem 20 Solution Six MATLAB Grade Mal Mpotong bao ASC210 Project 2 - www mounts/3033821021/problem/345710 problem solutionsew Brian Kouse Mpoki Course Content LMS Integration Documentation & Support AESC 210-SS21 > Project 2-Demographics > Problem 3 O solutions submitted (max 4) - . Modity the model derived in class to assess the following situation. Suppose an epideric (which shall remain nameless) raises all group death rates for giver period of time lle tworks much like the pulse function from last week & problem 2). This epidemic also lowers b2 birtheate. Assume migration is constant for group P2. SETUP parameters= [62.01,12,13,04,112,123,134] where b2 birth rate in group 2 di death rates in group PI o transition from group Pi to group PJ due to ageing Epleffect [b2Epifactor,drateEpifactor StartEp. tEndEpil, where b2Epifactor D2Epie b2b2Epifactor drateEpifactor d1 Epi=d1"drateEpifactor, etc Mann, constant migration rate for P2 Initconds [Pinit1 Pinit2. Pinit3 Pinit4) . timedata= [tinit,tfinal delt . RESULTS P1,P2 P3, P4, group time histories e Reset MATLAB Docu Grader Mail - Mpolokeng, Brian - Outlo > =1300742 ses described below using the following differentia nations has also been provided for reference. dP1/dt = BR*P2 -d1*P1 -t12*P1 dP2/dt = t12*P1 -d2*P2 -t23*P2 dP3/dt = t23*P2 -d3*P3 -t34*P3 dP4/dt = t34*P3 -d4*P4 igure 1: Differential Equations for Modeling 4 linked population

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Databases Questions!

Using C++ Programming C-code to integrate f(x) = e^(-x^2) elementof [-infinity, infinity] Use N of diff values, N number of steps/intervals. Print out all x_i, f_i = f(x_i) and the result. Determine...

Develop a C-code that numerically integrates the following function using N of different values, where N is the number of steps or intervals. Print out all [ see image-text ] and the final result....

Develop a C-code that numerically integrates the following function f(x) = e^(-x^2) elementof [-infinity, infinity] using N of different values, where Nis the number of steps or intervals. Print out...

Please Help me with algorithm I can't find a way to code this. Please send the code I will ever be grateful to you. For full pdf go to - send (ohiolink.edu) CHAPTER III IMPLEMENTATION OF THE EVENT...

Develop a C-code that numerically integrates the following function f(x) = sin (3x)/x elementof [-infinity, infinity] using N of different values, where N is the number of steps or intervals. Print...

ENGR 216 Final Project (Due in Class, December 11th, 2017 nolate submissios will be accepted) Choice 1 (last name with first letter from A to C) Develop a C-code that numerically integrates the...

Database systems(help needed urgently) thanks. Enrollment SIDSName SID CCode Midterm Final Total 100 Jones 100 BD445 70 77 150 Parks 150 BA200 65 89 200 Baker 93 Student Major Year Age History GR 21...

CODE MUST CONTAIN THE FOLLOWING FEATURES: (1) use of arrays, (2) use of pointers, (3) use of structure, (4) use of union, (5) use of functions and function calls, (6) formatted output on screen..CODE...

C++ HW Question Your program will simulate a simple change maker for a vending machine. It will start with a stock of coins and dollars. It will then repeatedly request the price for an item to be...

using trapezoidal rule Develop a C-code that numerically integrates the following function using N of different values, where N is the number of steps or intervals. Print out all xi,=f(x) and the...

Is Apple's explanation for why it adopted the new rules retrospectively clear (exhibit 1)? is it valid? arrangements that include software elements ("new accounting principles"). The new standards...

Prepare the Budgeted Income Statement that takes into account the loan. Assume that the Budgeted Income Statement of your business is as follows: Option I - Without a loan Budgeted Income Statement...

2 5 Multiple Choice 1 . 5 points A perpetuity pays $ 1 0 0 each and every year forever. The duration of this perpetuity will be q , if its yield is 9 % . 9 1 2 . 1 1 7 9 . 3 9 Clear my selection

Seved Help 14 Wisconsin Snowmobile Corp. is considering a switch to level production Cost efficiencies would occur under level production, and aftertax costs would decline by $31,500, but inventory...

From a Comparable Worth Standpoint, what is the situation with regard to Federal Gender-based Employee Pay Equity?

Provide an example of how drilling down further into information can yield new results.

What do Dimensions represent in OLAP Cubes?