this is a Matlab problem:-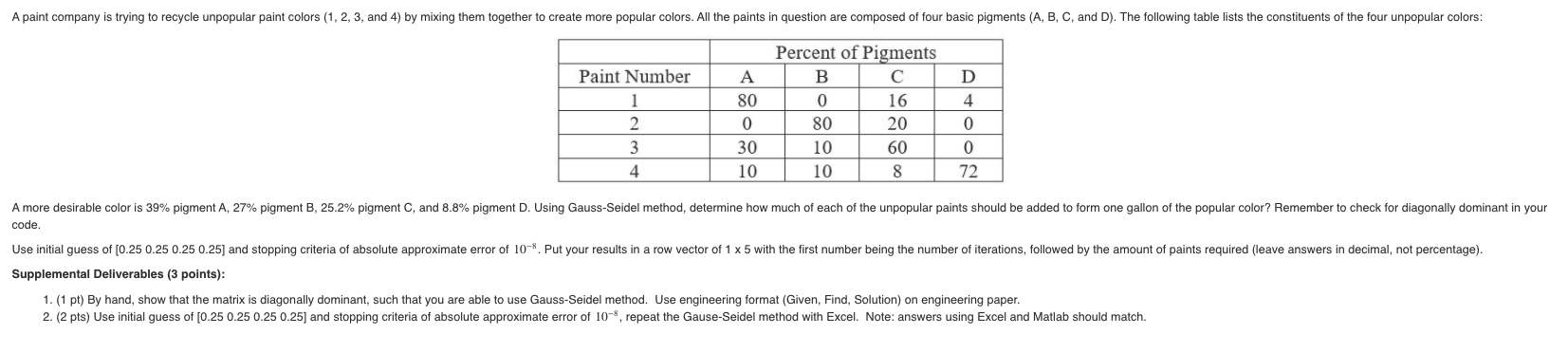please put the code with details. thanks I keep gettin it wrong

A paint company is trying to recycle unpopular paint colors (1, 2, 3, and 4) by mixing them together to create more popular colors. All the paints in question are composed of four basic pigments (A, B, C, and D). The following table lists the constituents of the four unpopular colors: Paint Number D 4 A 80 0 30 10 Percent of Pigments B 0 16 80 20 10 60 10 8 2 3 4 0 0 72 A more desirable color is 39% pigment A, 27% pigment B, 25.2% pigment C, and 8.8% pigment D. Using Gauss-Seidel method, determine how much of each of the unpopular paints should be added to form one gallon of the popular color? Remember to check for diagonally dominant in your code. Use initial guess of [0.25 0.25 0.25 0.25) and stopping criteria of absolute approximate error of 10-8. Put your results in a row vector of 1 x 5 with the first number being the number of iterations, followed by the amount of paints required leave answers in decimal, not percentage). Supplemental Deliverables (3 points): 1. (1 pt) By hand, show that the matrix is diagonally dominant, such that you are able to use Gauss-Seidel method. Use engineering format (Given, Find, Solution) on engineering paper. 2. (2 pts) Use initial guess of [0.25 0.25 0.25 0.25) and stopping criteria of absolute approximate error of 10-8, repeat the Gause-Seidel method with Excel. Note: answers using Excel and Matlab should match. A paint company is trying to recycle unpopular paint colors (1, 2, 3, and 4) by mixing them together to create more popular colors. All the paints in question are composed of four basic pigments (A, B, C, and D). The following table lists the constituents of the four unpopular colors: Paint Number D 4 A 80 0 30 10 Percent of Pigments B 0 16 80 20 10 60 10 8 2 3 4 0 0 72 A more desirable color is 39% pigment A, 27% pigment B, 25.2% pigment C, and 8.8% pigment D. Using Gauss-Seidel method, determine how much of each of the unpopular paints should be added to form one gallon of the popular color? Remember to check for diagonally dominant in your code. Use initial guess of [0.25 0.25 0.25 0.25) and stopping criteria of absolute approximate error of 10-8. Put your results in a row vector of 1 x 5 with the first number being the number of iterations, followed by the amount of paints required leave answers in decimal, not percentage). Supplemental Deliverables (3 points): 1. (1 pt) By hand, show that the matrix is diagonally dominant, such that you are able to use Gauss-Seidel method. Use engineering format (Given, Find, Solution) on engineering paper. 2. (2 pts) Use initial guess of [0.25 0.25 0.25 0.25) and stopping criteria of absolute approximate error of 10-8, repeat the Gause-Seidel method with Excel. Note: answers using Excel and Matlab should match