Question: this is a MATLAB question. Do not answer if you are not sure on how to do it correct. I have this matlab-code that solves
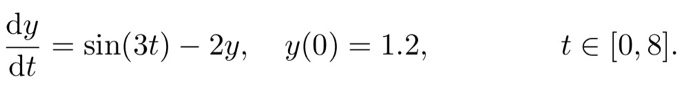

= sin(3+) 2y, y(0) = 1.2, t [0,8). dt n=5; for j=1:4 h=8 t=0:h:8; y=zeros(size(t)); y (1)=1.2; m=numel(y); exactsol=(1/65)*(93*exp(-2*t)-15*cos(3*t) +10*sin (3*t)); for i=1:m-1 f=sin( 3*t(i))-2*y(i); y(i+1)=y (i) + h*f; end n = n*2; el(j)=h; e(j)=norm(exactsol-y); plot (t,y) hold on end plot(t, exact sol); title('Exact solution and the four euler solutions') legend (n=5', 'n=10', 'n=20', 'n=40')
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


