This is a typical logistics model, with the corresponding network shown in the attached spreadsheet. Each net supplier's net outflow cannot exceed the capacity shown in its node, each net demander's net inflow must be at least the demand shown in its node, and each transshipment point must have a net outflow (and net inflow) of 0. The unit shipping costs are shown on the arcs, and the common arc capacity in the network is 1,100. The correct model and the optimal solution are shown in the attached spreadsheet. Let the common arc capacity vary from 600 to 3,000 in increments of 100. Which of the following is true of the resulting optimal solutions? Click here to reference the data needed to answer the question.

a. When the common arc capacity is 2,300 or less, the optimal total cost is greater than if there were no arc capacity constraints.

b. When the common arc capacity is at least 2,500, there are no arcs with flow equal to this capacity.

c. For each of these common arc capacities, each supplier's capacity constraint is binding except for supplier 1's, and all demand constraints are binding.

d. All of these choices are true.

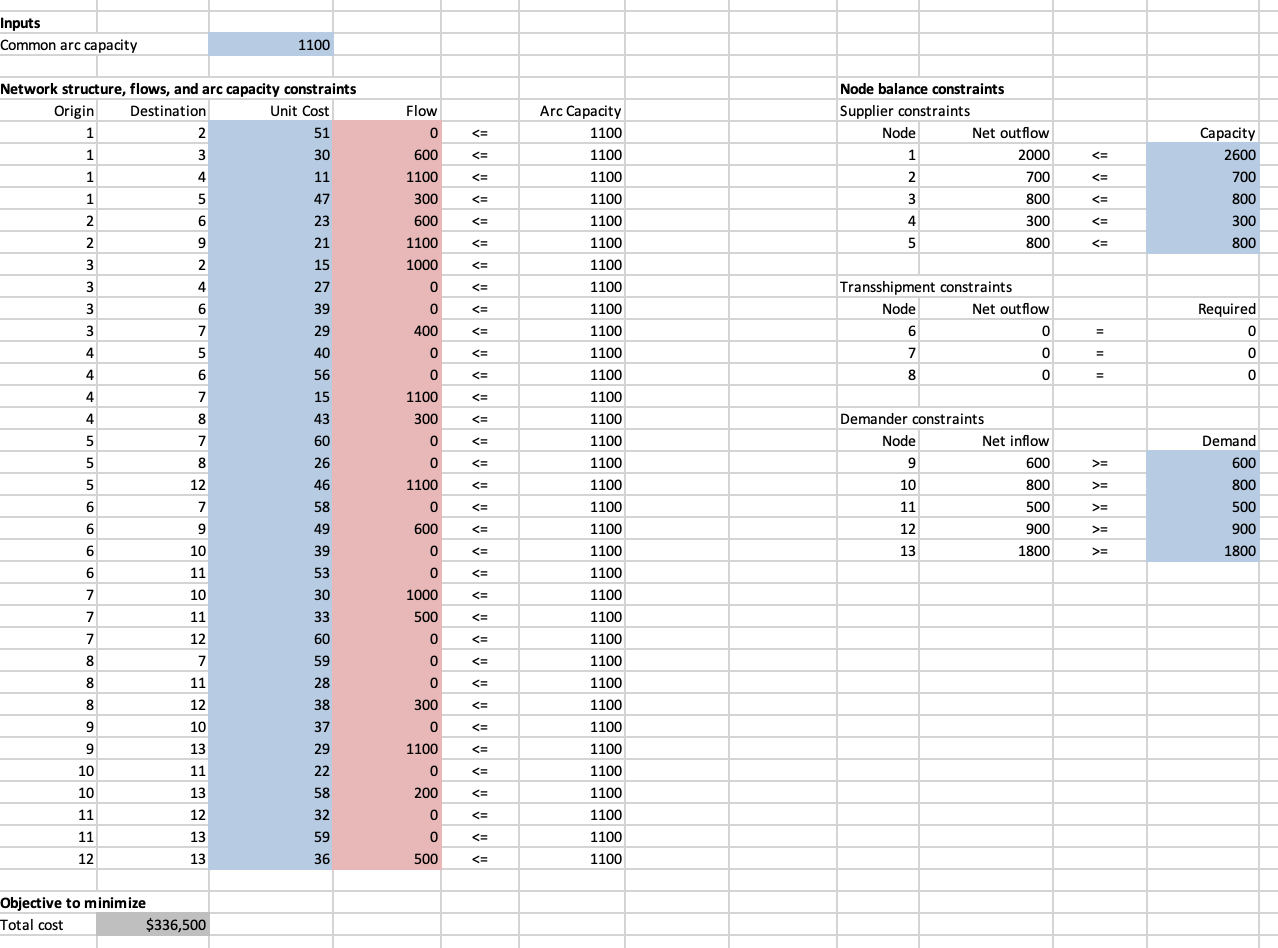
Inputs Common arc capacity 1100 Network structure, flows, and arc capacity constraints Node balance constraints \begin{tabular}{rl|r} 1000 & = & 600 \\ \hline 10 & 800 & >= & 800 \\ 11 & 500 & >= & 500 \\ \hline 12 & 900 & >= & 900 \\ \hline 13 & 1800 & >= & 1800 \end{tabular} 53 33 60 59 28 38 37 29 22 58 32 Objective to minimize Total cost $336,500 Inputs Common arc capacity 1100 Network structure, flows, and arc capacity constraints Node balance constraints \begin{tabular}{rl|r} 1000 & = & 600 \\ \hline 10 & 800 & >= & 800 \\ 11 & 500 & >= & 500 \\ \hline 12 & 900 & >= & 900 \\ \hline 13 & 1800 & >= & 1800 \end{tabular} 53 33 60 59 28 38 37 29 22 58 32 Objective to minimize Total cost $336,500