this is a vpython physics question. The initial code are given below.

from __future__ import division from visual import *

## Objects greenparticle = sphere(pos=vector(5,4,0), radius=0.25, color=color.green) ## Object that remains still blueparticle = sphere(pos=vector(-3,-2,0), radius=0.25, color=color.blue) ## Particle that will move trail = curve(color=blueparticle.color)

## Constants (you may need to change the values in this section) k = 0.3 ## interaction coefficient mblue = 5e-3 ## mass of blue particle (particle that will move). Change this as necessary.

## Initial conditions pblue = mblue*vector(800,800,0) ## initial momentum of blue particle. Change this as necessary.

## Time setup t = 0 deltat = 5e-6

while t

rate(1000000) ## Decrease this number if animation runs too quickly. Increase it or comment out if animation runs too slowly.

## Compute the net force on the blue particle

## Update the momentum of the blue particle

## Position update of the blue particle blueparticle.pos = blueparticle.pos + pblue/mblue*deltat

## Append trail to follow the blue particle trail.append(pos=blueparticle.pos)

## Increase time t = t + deltat

## Print final values

print("final position=", blueparticle.pos) print("final velocity=", pblue/mblue)

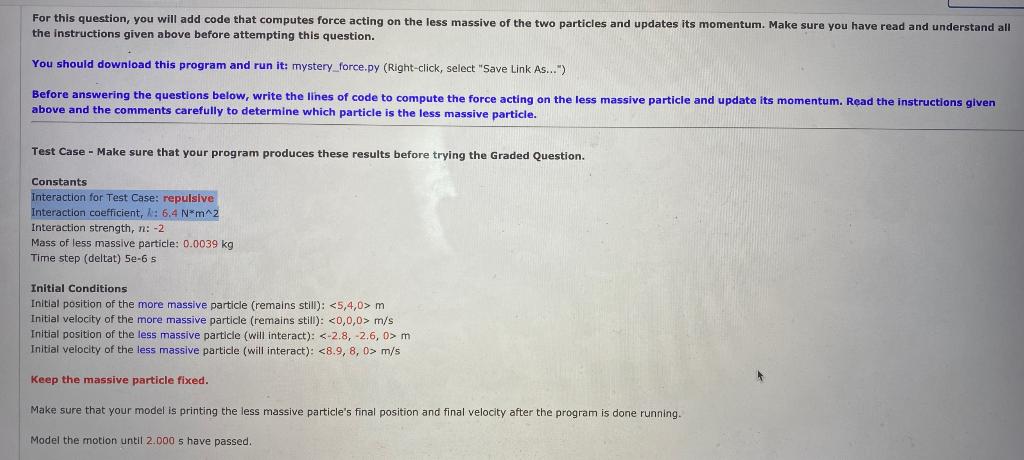
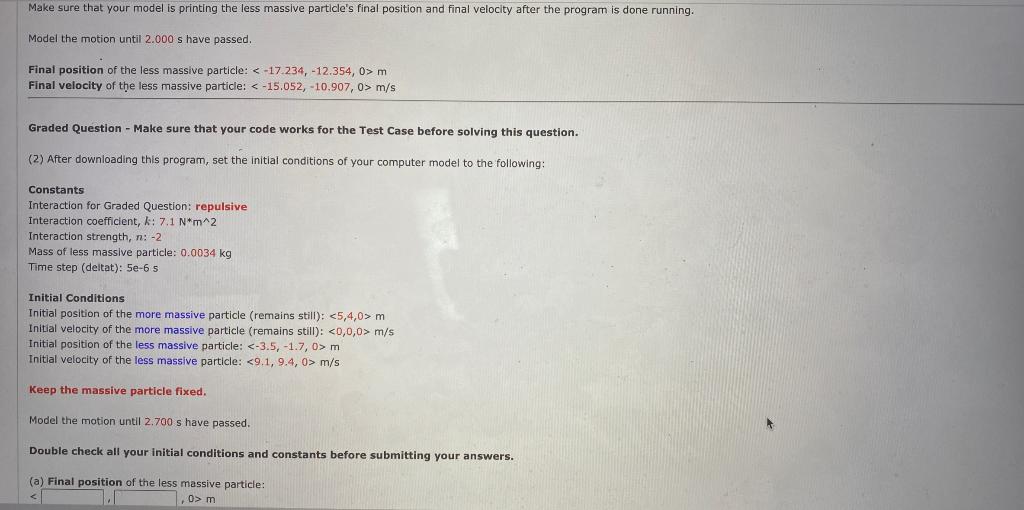
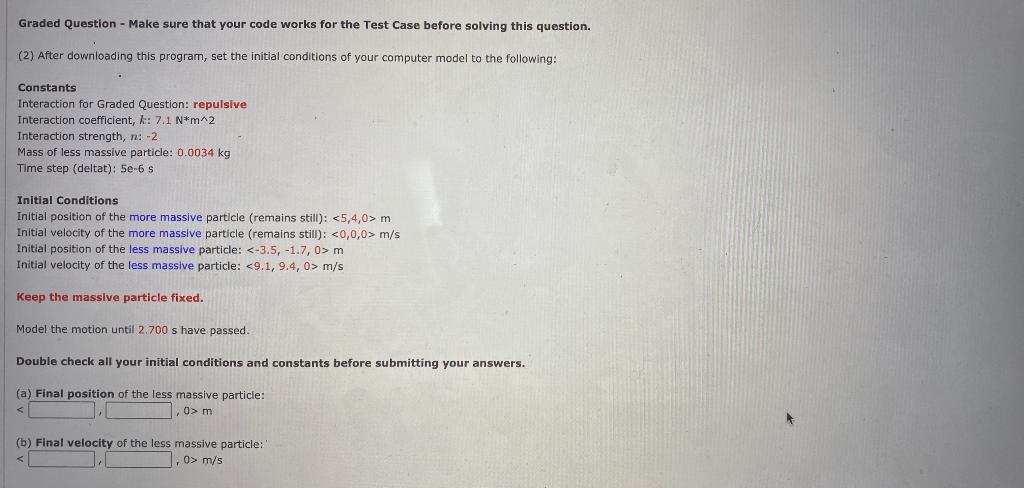
For this question, you will add code that computes force acting on the less massive of the two particles and updates its momentum. Make sure you have read and understand all the instructions given above before attempting this question. You should download this program and run it: mystery force.py (Right-click, select "Save Link As...") Before answering the questions below, write the lines of code to compute the force acting on the less massive particle and update its momentum. Read the instructions given above and the comments carefully to determine which particle is the less massive particle. Test Case - Make sure that your program produces these results before trying the Graded Question. Constants Interaction for Test Case: repulsive Interaction coefficient, : 6,4 N*m^2 Interaction strength, n: -2 Mass of less massive particle: 0.0039 kg Time step (deltat) 5e-6 s Initial Conditions Initial position of the more massive particle (remains still): m Initial velocity of the more massive particle (remains still): m/s Initial position of the less massive particle (will interact): m Initial velocity of the less massive particle (will interact): m/s Keep the massive particle fixed. Make sure that your model is printing the less massive particle's final position and final velocity after the program is done running Model the motion until 2.000 s have passed. Make sure that your model is printing the less massive particle's final position and final velocity after the program is done running. Model the motion until 2.000 s have passed. Final position of the less massive particle: m Final velocity of the less massive particle: m/s Graded Question - Make sure that your code works for the Test Case before solving this question. (2) After downloading this program, set the initial conditions of your computer model to the following: Constants Interaction for Graded Question: repulsive Interaction coefficient, k: 7.1 N*m^2 Interaction strength, n: -2 Mass of less massive particle: 0.0034 kg Time step (deltat): 5e-6 5 Initial Conditions Initial position of the more massive particle (remains still): m Initial velocity of the more massive particle (remains still): m/s Initial position of the less massive particle: m Initial velocity of the less massive particle: m/s Keep the massive particle fixed. Model the motion until 2.700 s have passed. Double check all your initial conditions and constants before submitting your answers. (a) Final position of the less massive particle: 0 m Graded Question - Make sure that your code works for the Test Case before solving this question. (2) After downloading this program, set the initial conditions of your computer model to the following: Constants Interaction for Graded Question: repulsive Interaction coefficient, k: 7.1 N*m^2 Interaction strength, n: -2 Mass of less massive particle: 0.0034 kg Time step (deltat): 5e-6 s Initial Conditions Initial position of the more massive particle (remains still): m Initial velocity of the more massive particle (remains still): m/s Initial position of the less massive particle: m Initial velocity of the less massive particle: m/s Keep the massive particle fixed. Model the motion until 2.700 s have passed. Double check all your initial conditions and constants before submitting your answers. (a) Final position of the less massive particle: m/s