this is about area between curves. Please provide step by step explanation.

1.

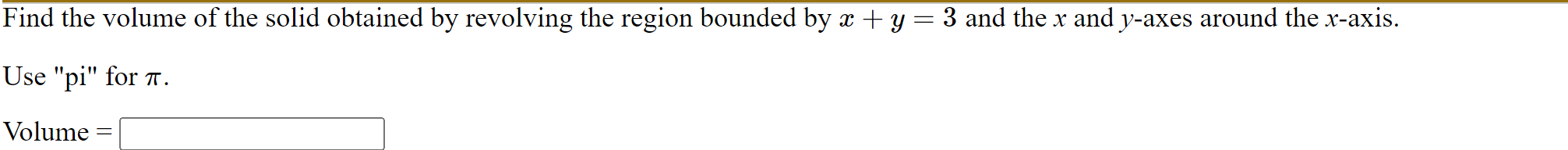
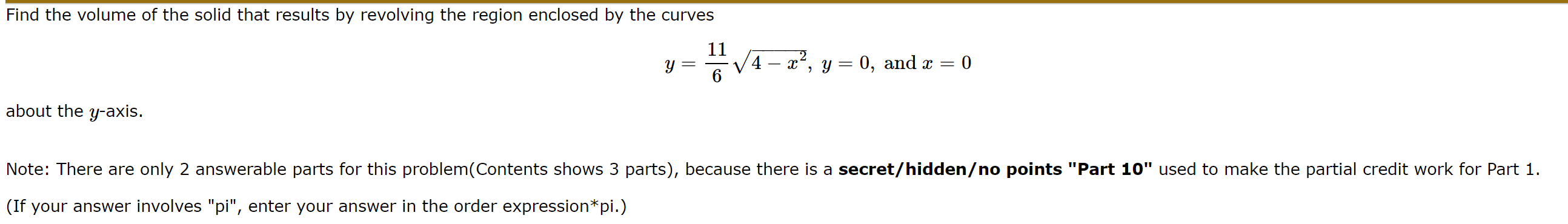
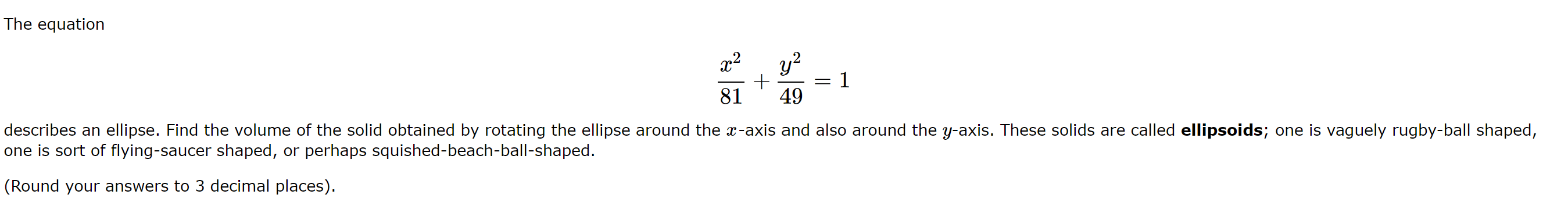
Find the volume of the solid obtained by revolving the region bounded by = 4 y = 3 and the x and y-axes around the x-axis. Use "pi" for 7. Volume = Find the volume of the solid that results by revolving the region enclosed by the curves 11 y=?\\/4fz ,y=0,andz =0 about the y-axis. Note: There are only 2 answerable parts for this problem(Contents shows 3 parts), because there is a secret/hiddeno points "Part 10" used to make the partial credit work for Part 1. (If your answer involves "pi", enter your answer in the order expression*pi.) Find the volume of the solid generated by rotating y = V2x+ N/ 8 about the x-axis from x = 1 to x = 4. (Round your answer to 3 decimal places).The equation 2 2 x_+y_:1 81 49 describes an ellipse. Find the volume of the solid obtained by rotating the ellipse around the z-axis and also around the y-axis. These solids are called ellipsoids; one is vaguely rugby-ball shaped, one is sort of flying-saucer shaped, or perhaps squished-beach-ball-shaped. (Round your answers to 3 decimal places). Hnowen - 2 - Y To find the volume of the solid formed by suevolving the sregion endosed by the wives yz ll 54-12, 4=0 and n= 0. about the y-anis we can use the disk method. first, find the limits of integration by setting y = ll Ju-us equal to y=0: 11 JU - ME = 0 6 This implies u = + 2 Now, the integral for the veline becomes: V = ITS" ( + Ju - /2 ) 2 du Simplify the integrand .. V = 17 9 2 121 (4 - 12 ) du V= ni S2 121 - 1212 dx 36 Now, integrate form by term: V = TT J.12Ln - 121 n 37 2 Evaluate at the upper and lower limit and subtract V= TT [ ( 121 12) - 121 ( 215 ) - 1 121(-2)+ 121 (-2) 3 iod 100 V = 1 242 - 3/42 + 242 + 242 9 9 V = 1 53.778 Andy Volume of the solid is 484. pi 9V = TT / 8+ 32 - 52 - 4 3 52 V= IT [ 40 02 +64- 352-8] V =1 [ 45 52 + 50 ] divide the numerator by the demomination: V = TT [ 15 02 + 14 ] multiply by IT and round to three decimal point. V2 11.21 2 cubic units The Volume of the solid generated by stating the given curve about the names fseem not to n=4 is applian 11.212 cubic units.Answer- 3+ To find the volume of the solid generated by rotating the (wwe y= Jin+, I about the manis from n=1 1= 4 , you can use the disk method. The formula for the volume if revolution using the disk method is given by ? V = ITS Cf ( nij 2 dn In this case, a-y b=4 and for) = Vent . So , the volume Vis given by V = IS " ( van + VM )2 dn Now, let's simplify this expression and then integrate it. V = TIS" ( 2n + 2ven # \\ + x ) du V = n Ju ( an + 2van * * + 2 ) an V = IT (4 ( ant 2 V 2 n2 ) dn V = IT 14 ( 2n+ 2 nv 2) dn Now integrate each term separately: V = n [ n2 + 2 n2 74 Evaluate the expression at n= 4 and nal the substract the result at nas from the result at n=4. V= [ (42 + 2.42) 342 ) - (/2 + 2:12 ) 7 V = 1 ( 8 + 32 ) - ( 2 + 2 2 ) ] V = TT [ 8 + 32 - 42 - 2 -7 V = IT 8+ 32 - 352_ 4 353 6- 352