Question: This is about Riemann Integral applications. Define increasing functions a, B, and y on [-1, 1 ] by a = X(o.1 1, B = X10.1
This is about Riemann Integral applications.
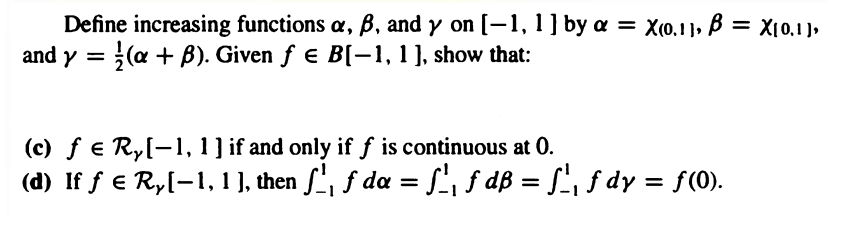
![y on [-1, 1 ] by a = X(o.1 1, B =](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/11/67303e65e1189_94967303e65b1ce8.jpg)
![X10.1 ], and y = (@ + B). Given f E B[-1,](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/11/67303e66474b7_95067303e6630d59.jpg)
Define increasing functions a, B, and y on [-1, 1 ] by a = X(o.1 1, B = X10.1 ], and y = (@ + B). Given f E B[-1, 1 ], show that: (c) f E R, [-1, 1 ] if and only if f is continuous at 0. (d) If f E Ry [-1, 1 ], then _, f da = _, f dB = ]_, f dy = f(0).IF P : Co. b) - IR is continuous Then & Is Kiemany integrable on [a. b). b -a 8 { N = ba 0 7 820 such thatStep - 1 Problem regarding the Riemann - Stieltjes integral and involves showing the equivalence of the integral with respect to particular step function for a bounded function f defined on [-1,1] The problem states: 1. Define increasing functions A Band y or [ 1 1] by d = x (0, 1] , B= Deco, 17 and y = + ( at B) . Heore re denots the characteristic function which is 0 on the interval excluding the point 1 ( food ) and including the point , ( foo p). 2 . Given afunction to that belongs to B[: 1 ] (the set of all bounded functions on the interval), we need to show two things." (o)FE Ry [-1, 17 hip and only if fo is continuous at c Q ) IN P E RY Ell], then S + da = [faB = jf dy = f (0) Let's address each pant separately.. Part @ : Explanation :- He need to show that A is Riemann - steffes integrable with respect to or if and only if fo is continuous at o. The function y only changes value at 0. For A to be Riemann - Stielties integrable with respect to yu the only potential point of discontinuity ion the integrators S must coincide with a point where I is continuous. This is because at points of discontinuity of the integrator, the Riemann- stieltjes integoal is sensitive to the value of A at that point
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


