This is based on a full-scale, real-world problem, where the Food and Agriculture Organization of theUN (FAO) commissioned the Institute of Business Research here at WMS to redesign the poverty linefood basket in the Solomon Islands, in order to minimize costs while meeting constraints on 17 typesof nutrients. Note that some of these constraints are minimums (e.g. the diet has to have at least 30grams of fiber per day), some are maximums (e.g. the diet cannot have more than 94 grams of fat perday) and one of them is an equality constraint (the diet must provide 2815 calories per day -to makethe resulting diet comparable to the existing basket of foods used in the food poverty line that alsoprovides 2815 calories). Note that the existing basket was set based on observing actual demand patternsofpoor households and this "cost of basic needs" basket would cost SBD$6429 per person per year fora diet that supplied 2815 calories per day (in NZD terms this is about $1200, so just over $3 per day). Your objective is to use the Simplex method of Linear Programming to redesign the food basket in acost minimizing way, and to interpret the shadow cost of various nutrients in the optimal solution. Ifyou wanted to read more about this use of LP for setting food poverty lines, but in a different setting,there is discussion in this working paper:

Instructions: The Excel file Diet.xlsx has a tab "Nutrient contents" that has data on the existing Cost-of-Basic-Needsfood poverty line basket for the Solomon Islands. The 50 foods in this basket provide 2815 calories perday, from an annual spending of SBD$6429. The decision variables are in cells B3-B52, and these areannual quantities of each food in the basket, where the initial quantities are based on the actual dietpattern ofpoor households in the Solomon Islands. Using the "sumproduct" command, the daily calories have been calculated for you.Note that the nutrientcontent is per 100grams, so the result of the sum-product command is divided by 36.5 (for 365 days ina year, but the nutrient contents are only in terms of 0.1 kg rather than per 1 kg, so give the nutrientsprovided by the diet for just one-tenth of a year, and dividing that by 36.5 gives a daily value). Youneed to use the sumproduct command to also calculate the daily consumption of each of the othernutrients (e.g. fibre, zinc) from the given diet.

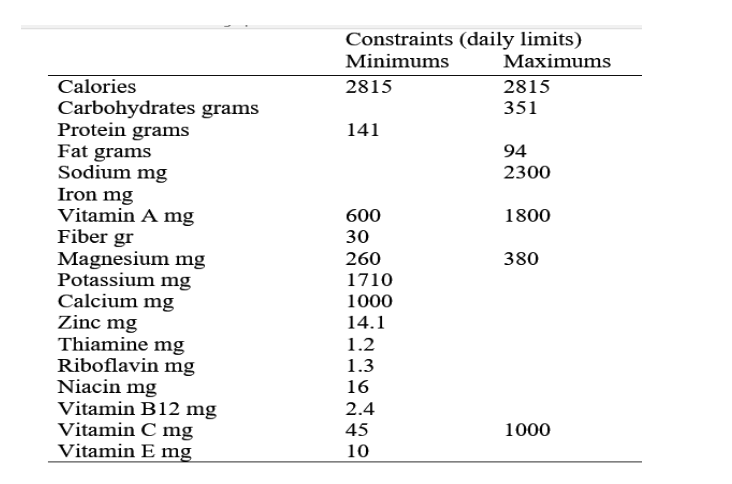
Next you need to enter the constraints. Some are maximums and some are minimums. The easiest wayto do this is to add two rows, with constraints, under the existing data. The constraints are as follows:

The objective function is in cell D54. You should instruct Solver that you want to minimize thisobjective function (subject to meeting the multiple constraints, where some are less than or equal to,some are greater than or equal to, and one is an equality). Note that you will have to enter constraintsinto the appropriate cells in your work sheet, and you will use the "Add" button in the solver dialog boxto add each constraint (note that there are more constraints than there are nutrients because some aresubject to both a minimum and a maximum). Calculate the cost-minimising diet, and when you useSolver, request an "Answer report" and a "Sensitivity report". Attach these reports to the Word fileand use their contents to help answer the questions below. (a) How many foods are in the cost-minimized diet and what is the annual cost of the diet? (b) How many of the nutritional constraints are binding? (c) From the Sensitivity Report, obtain the shadow price of Calories,and of Carbohydrate.Report theseand interpret them.

Calories Carbohydrates grams Protein grams Fat grams Sodium mg Iron mg Vitamin A mg Fiber gr Magnesium mg Potassium mg Calcium mg Zinc mg Thiamine mg Riboflavin mg Niacin mg Vitamin B12 mg Vitamin C mg Vitamin E mg Constraints (daily limits) Minimums 2815 141 600 30 260 1710 1000 14.1 1.2 1.3 16 2.4 45 10 Maximums 2815 351 94 2300 1800 380 1000