This is Difference equation. I need explanation of how the matrix (at the end) turn into second order difference equation at the end.

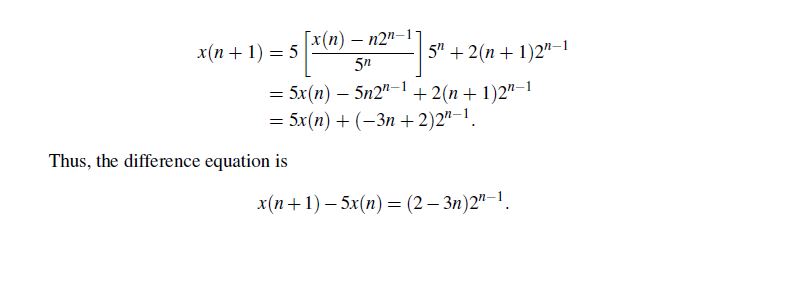
\fWe note that this can be worked out by computing rivet\") and then manipulating the two equations; The reason for only taking the rst order & is due to the existence of only one constant. [I Exampfe 2.22. Find the difference equation that its solution is given by xt) 2AM2 3n. Since the solution contains two constants, the corresponding difference equation is of order two. Thus, we must computexlfn + l) and x(n +2}. Replacing n with n + l and then r: with rt + 2 produoe the new relations mu} =A(n+ 1)33(n+1) .t-{n +2} =A{n+2}2 B{n+2). Eliminating A and B from the three equation given by x(n)=x[n + l), and xln +2) is equivalent to If\") n3 n x{n+ ]) {11+ \"2 {rr+ l) :0. an + 2) {n + 2)? {rr + 2} This simplies to the second order difference equation (n2 + n)x[n + 2) 2(n2 + Zulrln + l] + (n2 + 3n + 2}x(n] = D. 2.7 Recovery of Difference Equations Suppose we are given a sequence and asked to nd the recursive equation that the se quence satises. We have seen in previous sections that a solution to a kthorder differ ence equation contains k constants that are to be determined. In other words. the order of dte difference equation is equal to the number of arbitrary constants in its solution. Mathematically speaking. suppose we have the relationship xln} :fl-A}, wheieA is some constant. Then .r{n + l) =f{n+ LA]. Upon the elimination of A between these two equations. we obtain a relation between n,x(n), and xln+ 1) that we denote with F[n.x(n).x(n +1] 2 0. which represents the difference equation of interest. We illustrate the idea by several examples. This process can be repeated to accommodate solution that contains k constants of the form 25(13): f{n,Al.A2.- - 'f-llk). Example 2.2]. Find the difference equation that its solution is given by xtn} 2A5" +n2"-'. Since the solution contains one constant. the corresponding difference equation is of order one. Replacing n with n +1 produces the new relation 241:\" + l] = 5515\"] + {n + l)2" = 5A5\" + 2n:- + 1 )2'i1. Solving forA in the solution and then substituting it into the rightside of Ali: + 1] gives