this is the ipynb file: hello, this is the ipynb file: http://localhost:8888otebooks/Downloads/Counting%20for%20Probability.ipynb

please complete the text that says " # your code here" in artificial Intelligence

(python 3)

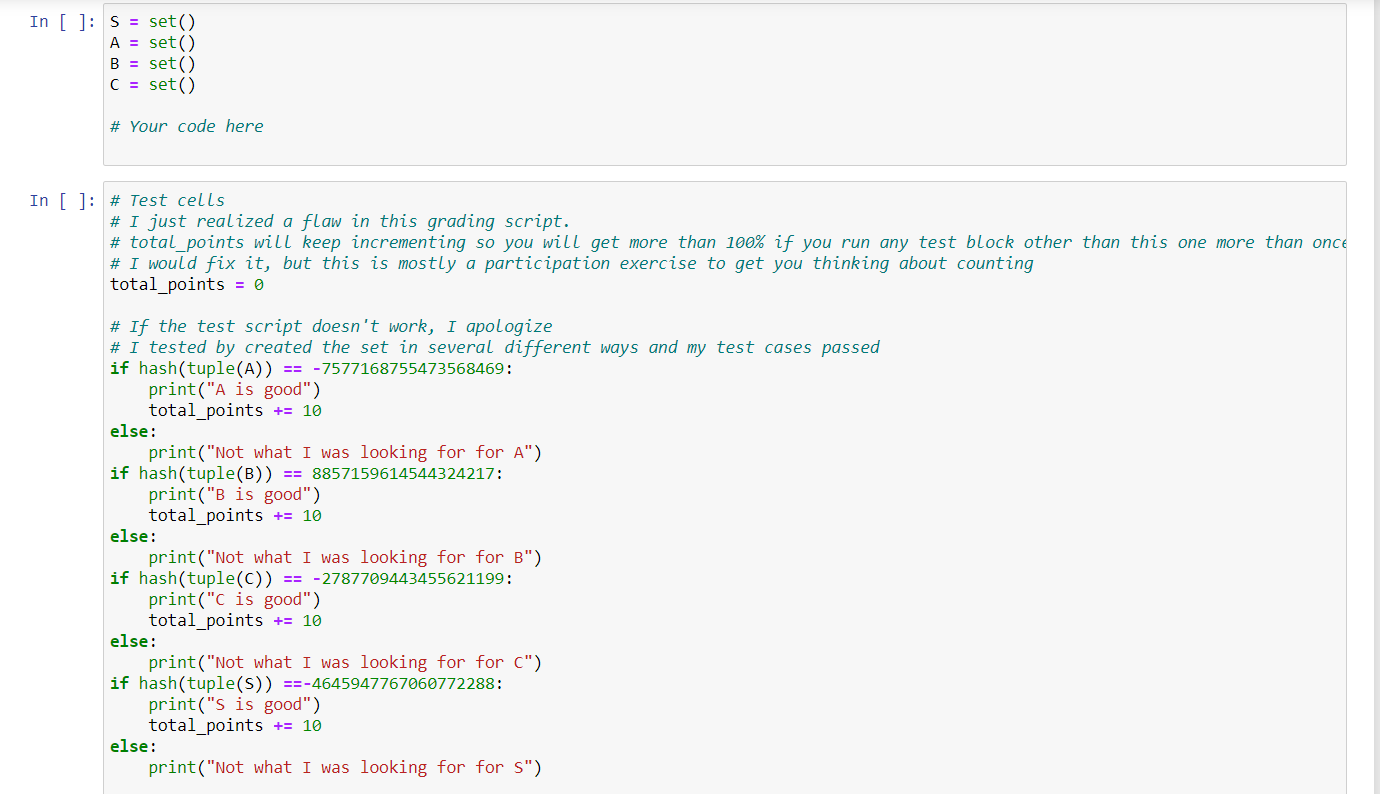
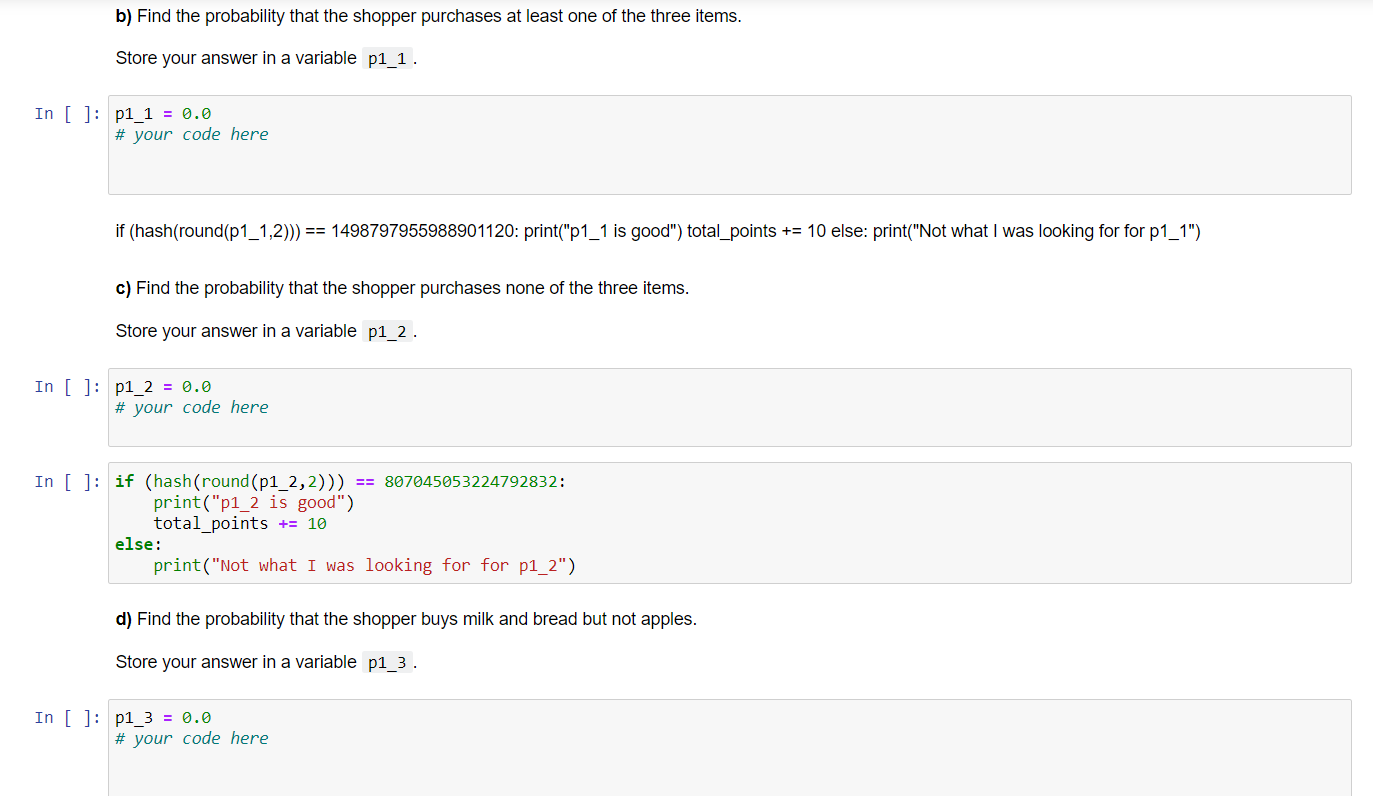
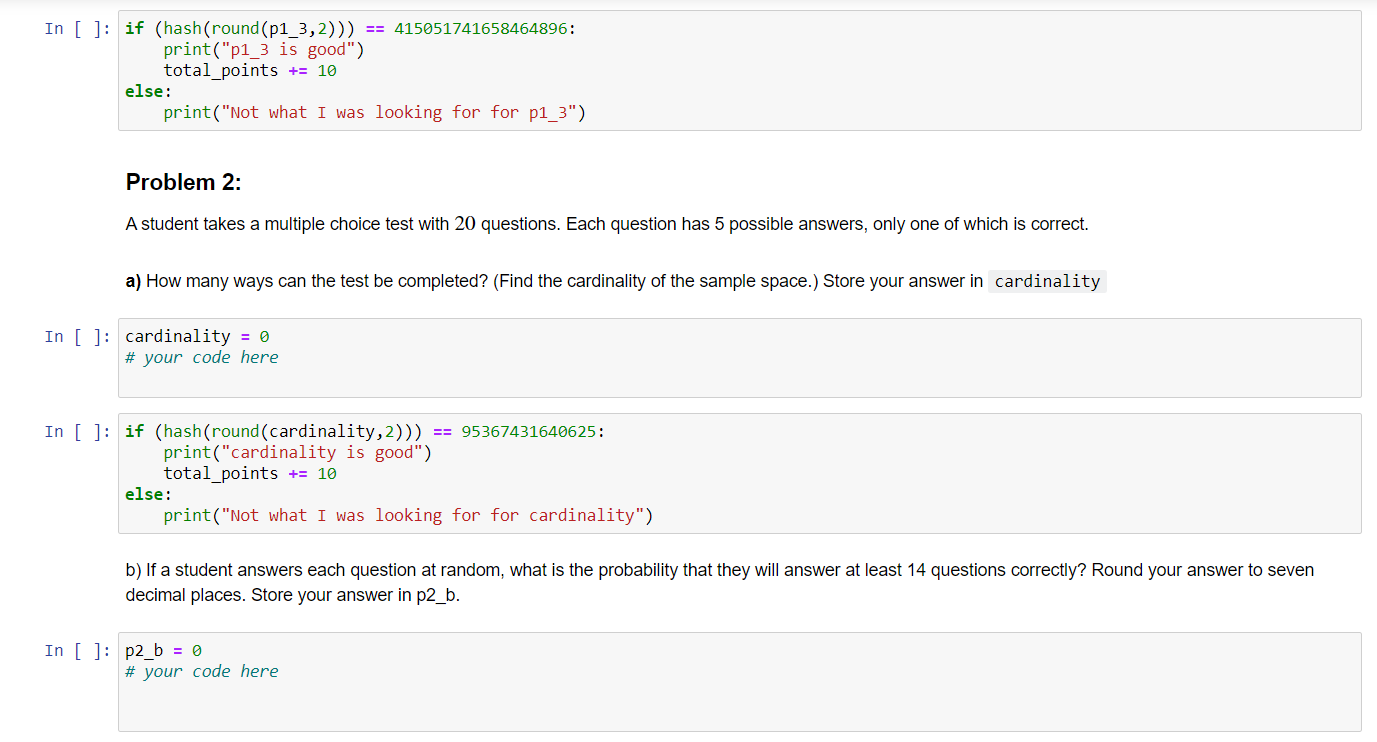
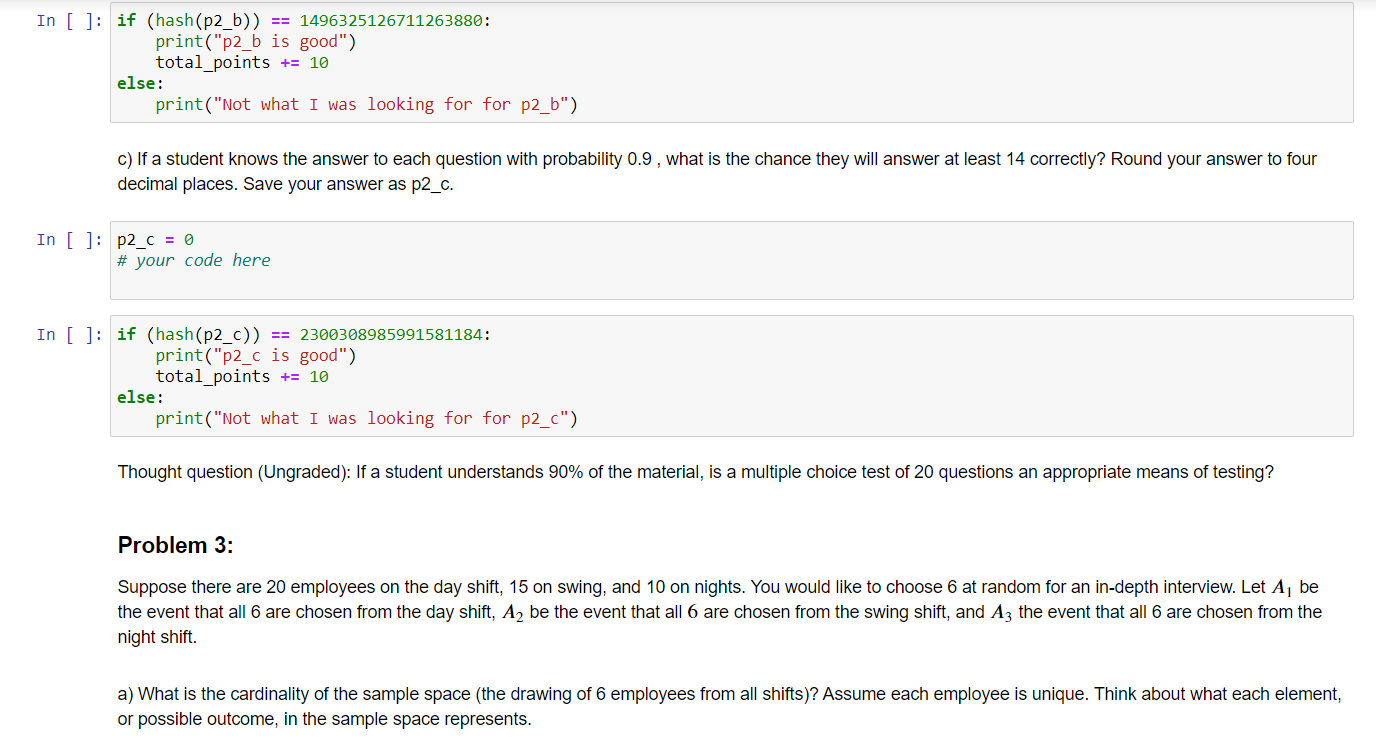
In this notebook you will apply the axioms of probability and use descriptive statistics to solve various problems. Please read each statement and answer all questions in the code blocks that contain "your code here". Problem 1: Suppose we are interested in the buying habits of shoppers at a particular grocery store with regards to whether they purchase apples, milk, andi'or bread. Now suppose 30% of all shoppers at this particular grocery store buy apples, 45% buy milk, and 40% buy a loaf of bread. Let A be the event that a randomly selected shopper buys apples, B be the event that the same randomly selected shopper buys milk, and C the event that they buy bread. Suppose we also know (from data collected) the following information: . The probability that the shopper buys apples and milk is 0.20. - The probability that the shopper buys milk and bread is 0.25. . The probability that the shopper buys apples and bread is 0.12. - The probability that the shopper buys all three items is 0.07. Use this information to answer the following questions. a) For our purposes, we will use a numeric representation for each event. For example, (010) would be an event in the sample space where a zero in the rst place represents no apples were bought while a 1 means they were. Similarly, the second place is the presence of milk and the third place of bread. The example given (010) represents the purchase of milk but not apples or bread. Insert into vector 5 the events that belong to the sample space. Then insert the events from the sample space that would correspond to A occuring into vector A . Repeat this with vector B for B and vector C for C. According to set notation, the sample space should look like this: S = [... }. However, due to data storage syntax in R, we will be storing these events in vectors. For example, for some arbitrary event W would be stored as follows W = c(010). c() is a command we can use to construct a vector where commas separate each entry. Complete the code below. Do not worry about the order in which events are placed in vector In [ ]: In [ ]: S = set() A = set() E = set() C = set() it Your code here # Test ceLLs # I just reaLized a flaw in this grading script. # totat_points wiLL keep incrementing so you will get more than 199% if you run any test block other than this one more than onC # I woaid fix it, but this is mostty a participation exercise to get you thinking about counting total_points = B # If the test script doesn't work, I apoLogize # I tested by created the set in several different ways and my test cases passed i-F hash(tuple(A) == -7577168755473568469: print("A is good") totalipoints += 19 else: print("Not what I was looking for for A") if hash(tuple(B)) == 8857159614544324217: print("B is good") totalipoints += 19 else: print("Not what I was looking for for B") if hash(tuple(c)) == -2787769443455621199: print("c is good") totalipoints += 19 else: print("Not what I was looking for for C") if hash(tuple(5) ==-4645947767666772288: print("5 is good") totalipoints += 19 else: print("Not what I was looking for for S") In [ ]: In [ ]: In [ ]: In [ ]: b) Find the probability that the shopper purchases at least one of the three items. Store your answer in a variable p1_1 . p171 = 0.6 # your code here if (hash(round(p1_1 ,2))) == 1498797955966901120: print("p1_1 is good") total_points += 10 else: print("Not what I was looking for for p1_1 ") c) Find the probability that the shopper purchases none of the three items. Store your answer in a variable p1_2 . p172 = 0.6 # your code here if (hash(round(p172,2))) == 867645653224792832: print(\"pl_2 is good") totalipoints += 1% else: print(\"Not what I was looking for For p1_2") (I) Find the probability that the shopper buys milk and bread but not apples. Store your answer in a variable p173 . p1_3 = 6.6 # your code here In [ ]: In [ ]: In [ ]: In [ ]: if (hash(round(p1_3,2))) == 415951741658464896: print("p1_3 is good") total_points += 16 else: print("Not what I was looking for for p1_3") Problem 2: A student lakes a multiple choice test with 20 questions. Each question has 5 possible answers, only one of which is correct. a) How many ways can the test be completed? (Find the cardinality of the sample space.) Store your answer in cardinality cardinality = B # your code here if (hash(round(cardinality,2))) == 95367431648625: print("cardinality is good") total_points += 16 else: print("Not what I was looking for for cardinality") b) If a student answers each question at random, what is the probability that they will answer at least '14 questions correctly? Round your answer to seven decimal places. Store your answer in p243. p2_b = e # your code here In [ ]:I In [ ]: In [ ]: i-F (hash(p27b)) == 1496325126711263886: print("p27b is good") total_point5 += 16 else: print("Not what I was looking for for p27b") c) If a student knows the answer to each question with probability 0.9 , what is the chance they will answer at least '14 correctly? Round your answer to four decimal places. Save your answer as p27c. p27c = e # your code here if (hash(p2_c)) == 2366368985991581184: print("p27c is good") total_point5 += 19 else: print("Not what I was looking for" for\" pzic") Thought question (Ungraded): If a student understands 90% of the material, is a multiple choice test of 20 questions an appropriate means of testing? Problem 3: Suppose there are 20 employees on the day shift, 15 on swing, and 10 on nights. You would like to choose 6 at random for an in-depth interview. Let A1 be the event that all 6 are chosen from the day shift, A2 be the event that all 6 are chosen from the swing shift, and A3 the event that all 6 are chosen from the night shift. a) What is the cardinality of the sample space (the drawing of 5 employees from all shifts)? Assume each employee is unique. Think about what each element, or possible outcome, in the sample space represents. In [ ]: In [ ]: In [ ]: In [ ]: In [ ]: Size = e # your code here if (hash(str'(size))) == -2811962898395558376: print("Size is good\") total_point5 += 16 else: print("Not what I was looking for for Size") b) Assuming that each employee is chosen with equal probaiblity, what is the probability that all 6 chosen employees work the day shift? Note that the employees are chosen sequentially, not all at once. Round your answer to 5 decimal places. Save your answer as PiAllDay. Thought question (ungraded): If you hired a consultant to do this interview and all 6 employees were chosen from the day shift, what would you be likely to conclude? PiAllDay = B # your code here if (hash(P_AllDay)) == 16975812723857184: print("P_AllDay is good") total_point5 += 16 else: print("Not what I was looking for for P_AllDay") c) What is the probability that all 6 workers are selected from the same shift? Again, assume the employees are selected sequentially and not all at once. Round your answer to four decimal places. Save your answer as P_A||Same. P_AllSame = a # your code here In [ ]: if (hash(P_Allsame) ) == 12451552249753948: print("P_Allsame is good") total_points += 10 else : print("Not what I was looking for for P_Allsame") Thought question (Ungraded): Let B, be the event that no one from the day shift is selected, By the event that no one from the swing shift is selected, and B3 the event that no one from the night shift is selected. How is Af defined? Is it related to B, or BY ? It's very important to carefully define the events of interest so that you know you are calculating the correct probability. d) Find the probability that at least one of the shifts will be unrepresented in the sample of 6 workers. Round your answer to four decimal places. Save your answer as P_NoneOfOneShift . Hint: We want to solve P(B, U B2 U B3). To solve this, it may help to make a venn diagram for these events. Make sure you don't overcount the overlapping areas of this venn diagram! In [ ]: P_NoneOfOneShift = 0.0 # your code here In [ ]: if (hash(P_NoneofoneShift)) == 665235708158150656: print("P_NoneOfOneShift is good") total_points += 10 else : print("Not what I was looking for for P_NoneofoneShift") In [ ]: print("You might want to clean and run everything again to get this to work right") print(f"Total points (assuming clean run of tests) {total_points}") print(f"Score in percent {round(total_points/110*100,2) }%")