***THIS MUST BE DONE IN MATLAB***

1.) Determine the shearing transformation matrix that shears 3 units in the vertical direction. Plot the original square together with the sheared square. Use axis([-2,4,-2,4]);. Add a grid, a legend and a title (similarly to EXAMPLE 4). Include the M-file as well as the figure.

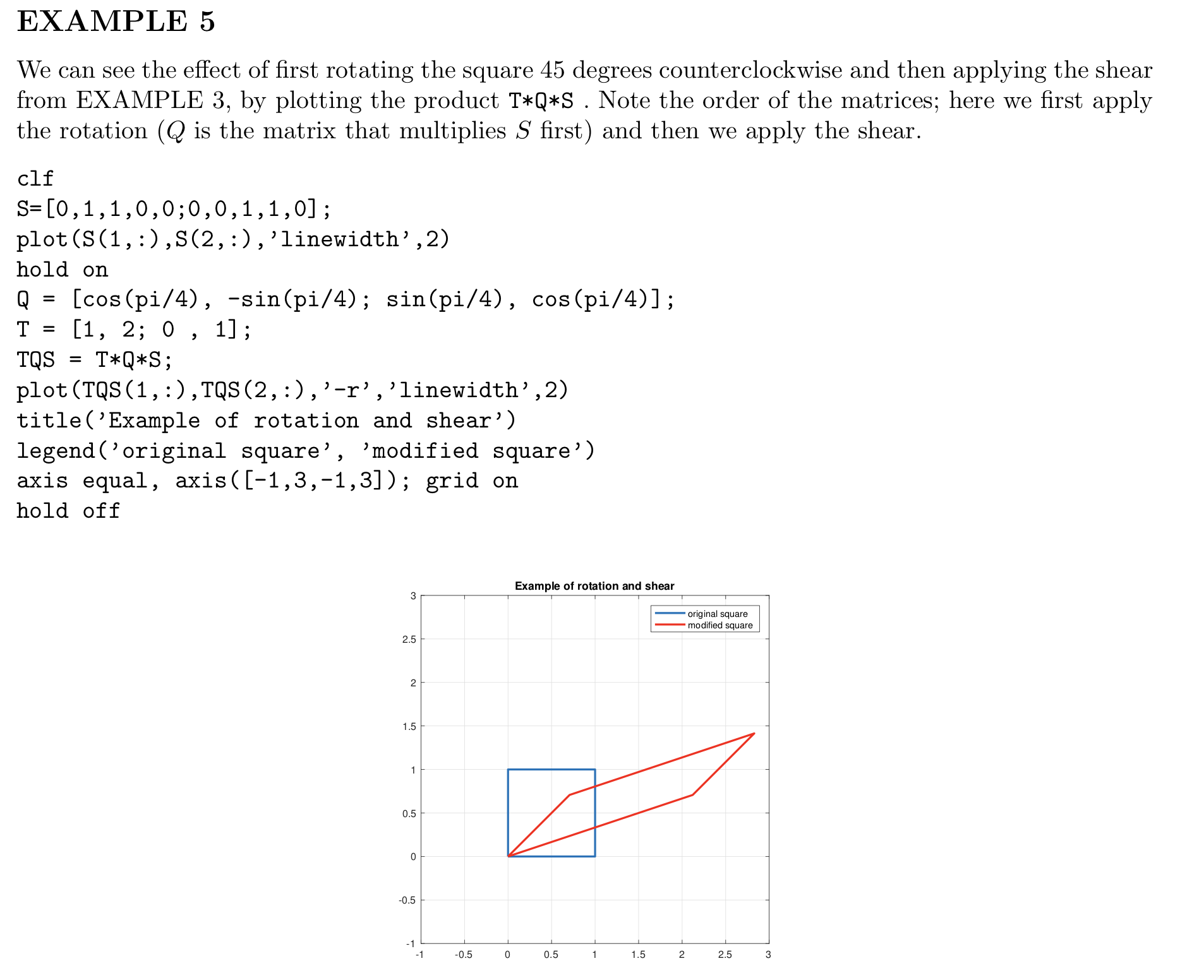
2. Consider the original square S. First apply the shear transformation from EXAMPLE 4 and then rotate the square 45 counterclockwise. Plot the resulting figure (together with the original square) and compare with the plot in Example 5. Are the results the same? Does the order of the transformations matter?

Include the M-file as well as the figure and dont forget to answer all questions. Hint: Here you want to apply the shear first, then rotate, whereas in Example 5 the square is first rotated and then the shear is applied. To do this, TQS = T*Q*S, where Q is the rotation matrix and T is the shearing transformation matrix. So, if you want to first shear and then rotate, in what order will you multiply the matrices?

Reflection Matrices and Combinations of Transformations EXAMPLE 4. Reflecting the triangle about the line at 45 degrees and then rotating it /4 Radians CCW >> clf >> plot(T(1,:),T(2,:),'linewidth',2) >> hold on >>Q [cos(pi/4), -sin(pi/4); sin(pi/4), cos(pi/4)]; >>plot(QRT(1,:),QRT(2,:),'-r','linewidth',2) >> title('Example of Reflexion and Rotation') >> legend('original triangle','modified triangle') >> grid on >>axis equal >>hold off Reflection Matrices and Combinations of Transformations EXAMPLE 4. Reflecting the triangle about the line at 45 degrees and then rotating it /4 Radians CCW >> clf >> plot(T(1,:),T(2,:),'linewidth',2) >> hold on >>Q [cos(pi/4), -sin(pi/4); sin(pi/4), cos(pi/4)]; >>plot(QRT(1,:),QRT(2,:),'-r','linewidth',2) >> title('Example of Reflexion and Rotation') >> legend('original triangle','modified triangle') >> grid on >>axis equal >>hold off