1. This problem

   		does not have a feasible solution.
   		has alternative optimal solutions.
   		has an unbounded objective function.
   		has a unique, i.e., a single, optimal solution.
   		none of the above.

QUESTION 15

1. The point (90/19, 20/19) is

   		feasible but not optimal.
   		infeasible.
   		optimal.
   		not an intercept point.
   		none of the above.

QUESTION 16

1. The point (6, 3) is

   		feasible.
   		not on the boundary of the feasible region.
   		not optimal.
   		all of the above.
   		none of the above.

QUESTION 17

1. The point (3, 1) satisfies

   		the first constraint but not the other two.
   		the second constraint but not the other two.
   		the third constraint but not the other two.
   		all three constraints.
   		none of the above.

QUESTION 18

1. The point (10, 0) is

   		feasible but not optimal.
   		an optimal solution.
   		infeasible.
   		not on the boundary of the feasible region.
   		none of the above.

QUESTION 19

1. The value of the objective function at the point (90/19, 20/19) is

   		40
   		360/19
   		400/19
   		not determined
   		none of the above

QUESTION 20

1. The optimal objective function value is

   		4
   		20
   		40
   		80
   		cannot be determined

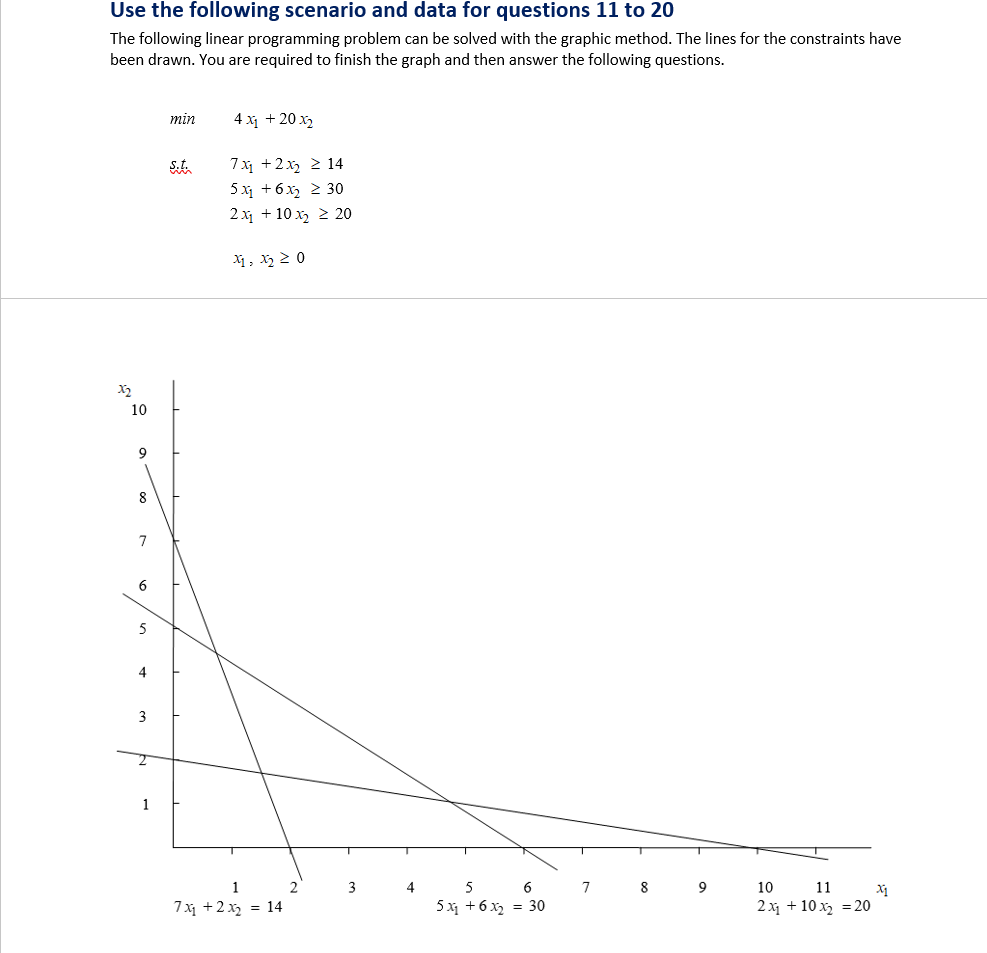
Use the following scenario and data for questions 11 to 20 The following linear programming problem can be solved with the graphic method. The lines for the constraints have been drawn. You are required to finish the graph and then answer the following questions. min 4 x1 + 20 x2 S.t. 7 X1 + 2x2 > 14 5x1 +6x2 > 30 2 x1 + 10 x2 > 20 X1, X220 22 10 9 8 7 6 5 4 3 2 1 3 4 7 8 9 X1 1 2 7 X1 + 2 x2 = 14 6 5X+6x2 = 30 10 11 2 x1 + 10 x2 = 20