this problem has 2 parts, could someone please help me with this.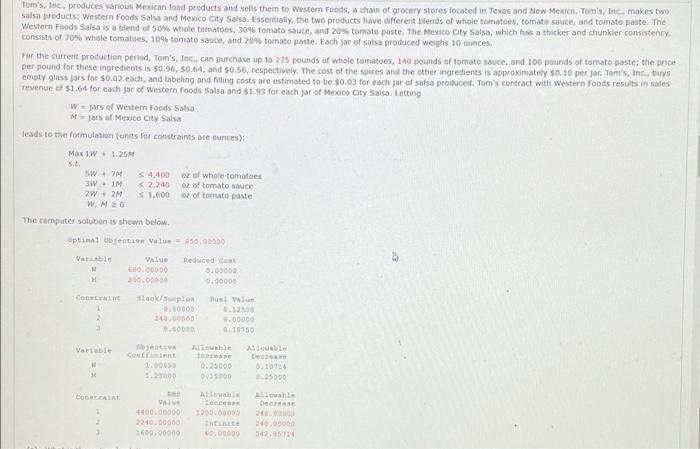

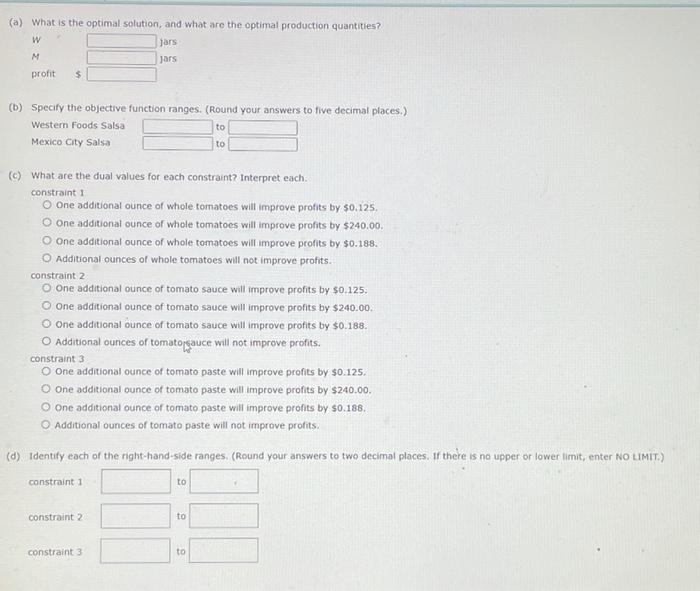
Tom's, Inc., produces various Mexican food products and sells them to Western Foods, a chain of grocery stores located in Texas and New Mexico. Tom's, Inc. makes two salsa products: Western Foods Salsa and Mexico City Salsa. Essentially, the two products have different blends of whole tomatoes, tomato sauce, and tomato paste. The Western Foods Salsa is a blend of 50% whole tomatoes, 30% tomato sauce, and 20% tomato paste. The Mexico City Salsa, which has a thicker and chunkier consistency, consists of 70% whole tomatoes, 10% tomato sauce, and 20% tomato paste. Each jar of salsa produced weighs 10 ounces. For the current production period, Tom's, Inc., can purchase up to 275 pounds of whole tomatoes, 140 pounds of tomato sauce, and 100 pounds of tomato paste; the price per pound for these ingredients is $0.96, $0.64, and $0.56, respectively. The cost of the spices and the other ingredients is approximately $0.10 per jar. Tom's, Inc., buys empty glass jars for $0.02 each, and labeling and filling costs are estimated to be $0.03 for each jar of salsa produced. Tom's contract with Western foods results in sales revenue of $1.64 for each jar of Western Foods Salsa and $1.93 for each jar of Mexico City Salsa. Letting W Jars of Western Foods Salsa M jars of Mexico City Salsa leads to the formulation (units for constraints are ounces): Max 1W 1.25M s.t. $4,400 oz of whole tomatoes SW 7M 3W 1M 2,240 oz of tomato sauce 2W + 2M 1,600 oz of tomato paste W, M 20 The computer solution is shown below. Optimal Objective Value $50.00000 Variable Reduced Cost M Value 600.00000 200.00000 0.00000 M 0.00000 Constraint Dusi Value 1 0.12500 2 0.00000 3 0.18750 Allowable Allowable Variable Increase Decrease 0.25000 0.10714 0.15000 0.25000 Allowable Allowable Constraint occas Decrease 1 1200.00000 240.00000 2 Inte 240.00000 3 0.00000 34295714 3140k/Surplus 0.00000 240.00000 0.00000 Objective Coefficient 1.00000 1.25000 682 Value 4400.00000 2240.00000 2600,00000 (a) What is the optimal solution, and what are the optimal production quantities? W jars M Jars profit $ (b) Specify the objective function ranges. (Round your answers to five decimal places.) Western Foods Salsa to Mexico City Salsa to (c) What are the dual values for each constraint? Interpret each. constraint 1 O One additional ounce of whole tomatoes will improve profits by $0.125. O one additional ounce of whole tomatoes will improve profits by $240.00. O One additional ounce of whole tomatoes will improve profits by $0.188. O Additional ounces of whole tomatoes will not improve profits. constraint 2 O one additional ounce of tomato sauce will improve profits by $0.125. O one additional ounce of tomato sauce will improve profits by $240.00. O one additional ounce of tomato sauce will improve profits by $0.188. O Additional ounces of tomato sauce will not improve profits. constraint 3 O One additional ounce of tomato paste will improve profits by $0.125. O one additional ounce of tomato paste will improve profits by $240.00. O one additional ounce of tomato paste will improve profits by $0.188. O Additional ounces of tomato paste will not improve profits. (d) Identify each of the right-hand-side ranges. (Round your answers to two decimal places. If there is no upper or lower limit, enter NO LIMIT.) constraint 1 to constraint 2 to constraint 3 to