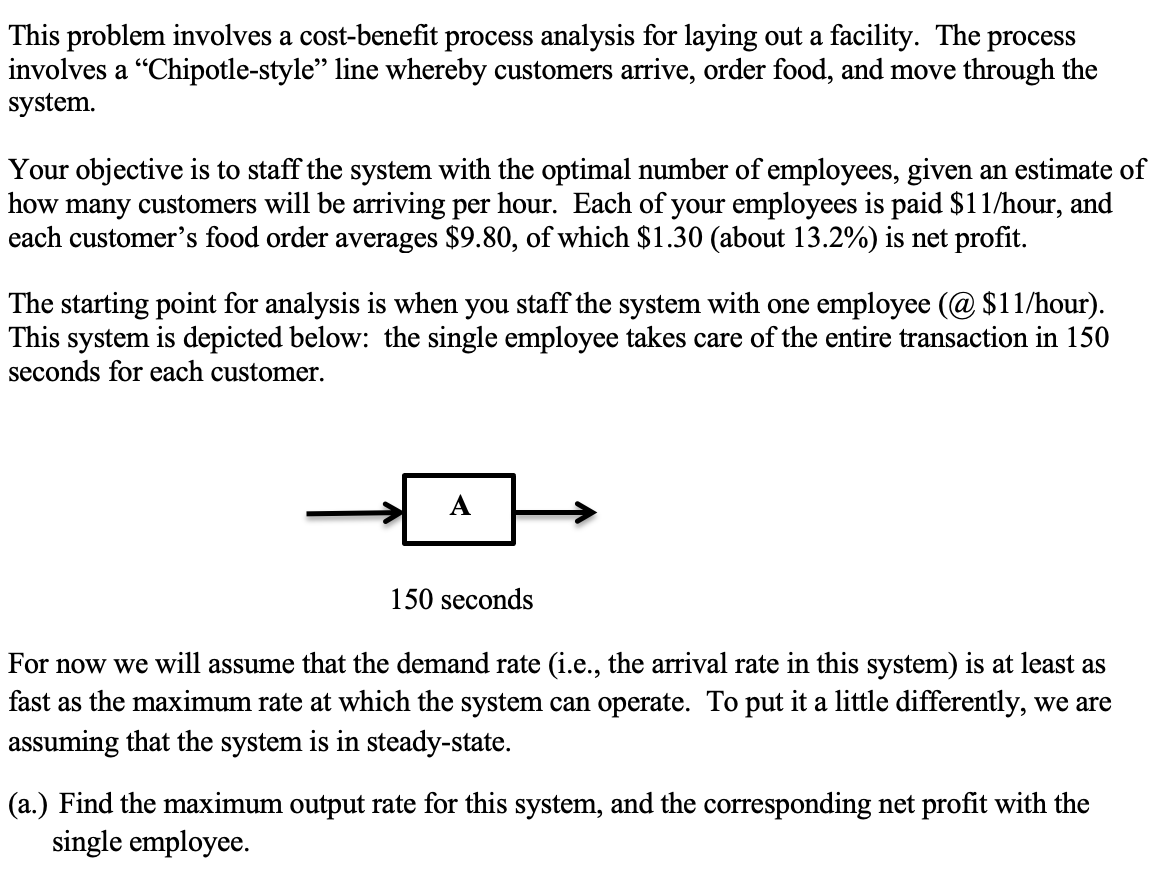
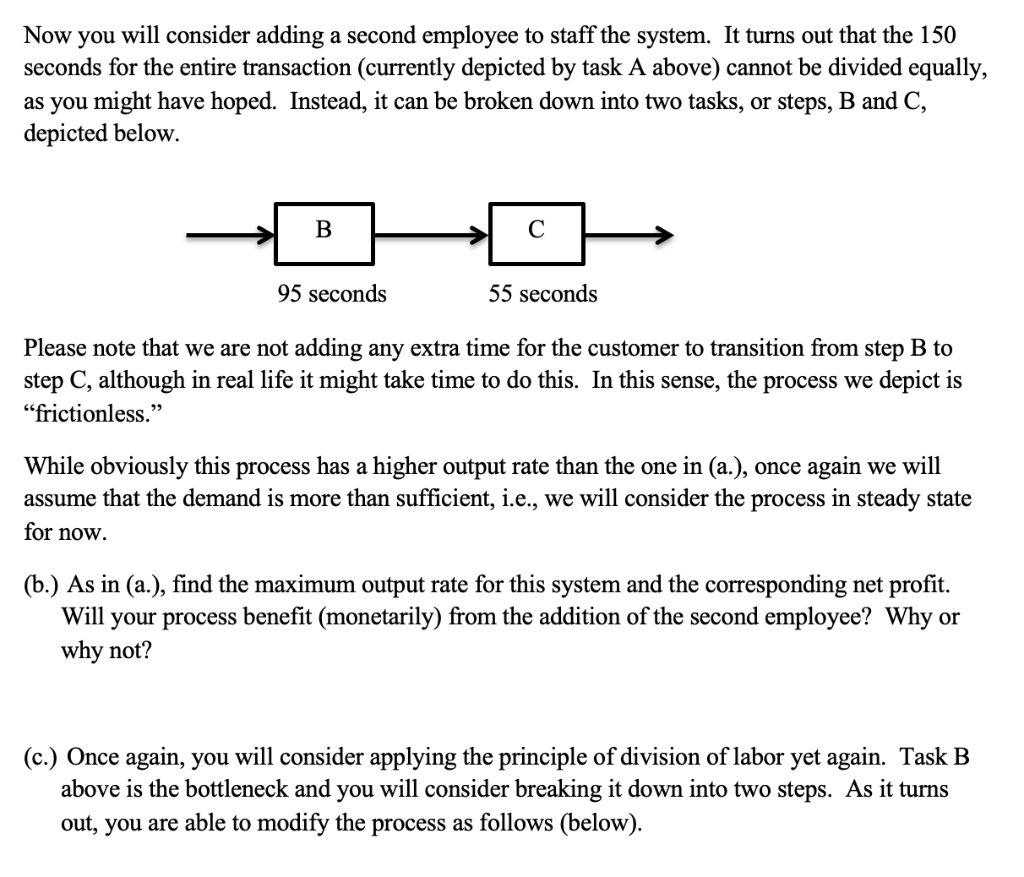
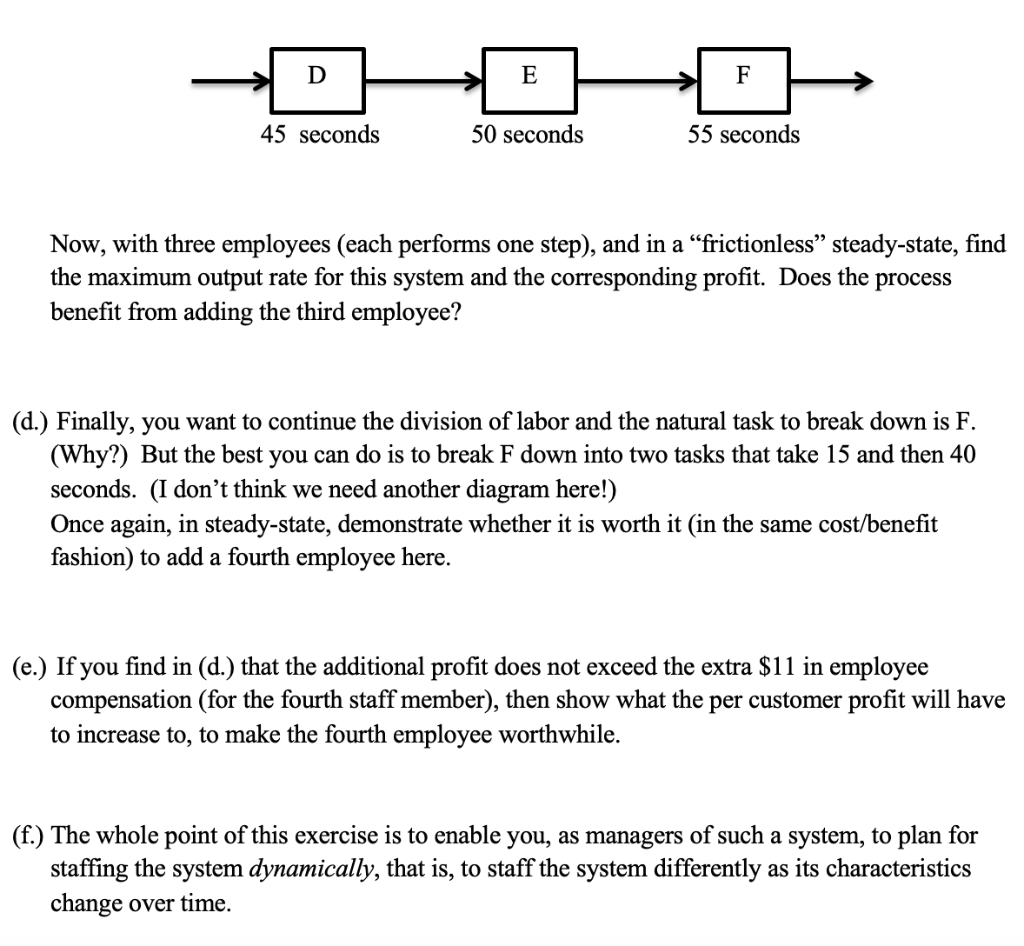
This problem involves a cost-benefit process analysis for laying out a facility. The process involves a Chipotle-style line whereby customers arrive, order food, and move through the system. Your objective is to staff the system with the optimal number of employees, given an estimate of how many customers will be arriving per hour. Each of your employees is paid $11/hour, and each customer's food order averages $9.80, of which $1.30 (about 13.2%) is net profit. The starting point for analysis is when you staff the system with one employee (@ $11/hour). This system is depicted below: the single employee takes care of the entire transaction in 150 seconds for each customer. A 150 seconds For now we will assume that the demand rate (i.e., the arrival rate in this system) is at least as fast as the maximum rate at which the system can operate. To put it a little differently, we are assuming that the system is in steady-state. (a.) Find the maximum output rate for this system, and the corresponding net profit with the single employee. Now you will consider adding a second employee to staff the system. It turns out that the 150 seconds for the entire transaction (currently depicted by task A above) cannot be divided equally, as you might have hoped. Instead, it can be broken down into two tasks, or steps, B and C, depicted below. B 95 seconds 55 seconds Please note that we are not adding any extra time for the customer to transition from step B to step C, although in real life it might take time to do this. In this sense, the process we depict is frictionless. While obviously this process has a higher output rate than the one in (a.), once again we will assume that the demand is more than sufficient, i.e., we will consider the process in steady state for now. (b.) As in (a.), find the maximum output rate for this system and the corresponding net profit. Will your process benefit (monetarily) from the addition of the second employee? Why or why not? (c.) Once again, you will consider applying the principle of division of labor yet again. Task B above is the bottleneck and you will consider breaking it down into two steps. As it turns out, you are able to modify the process as follows (below). D E F 45 seconds 50 seconds 55 seconds Now, with three employees (each performs one step), and in a frictionless steady-state, find the maximum output rate for this system and the corresponding profit. Does the process benefit from adding the third employee? (d.) Finally, you want to continue the division of labor and the natural task to break down is F. (Why?) But the best you can do is to break F down into two tasks that take 15 and then 40 seconds. (I don't think we need another diagram here!) Once again, in steady-state, demonstrate whether it is worth it (in the same cost/benefit fashion) to add a fourth employee here. (e.) If you find in (d.) that the additional profit does not exceed the extra $11 in employee compensation (for the fourth staff member), then show what the per customer profit will have to increase to, to make the fourth employee worthwhile. (f.) The whole point of this exercise is to enable you, as managers of such a system, to plan for staffing the system dynamically, that is, to staff the system differently as its characteristics change over time