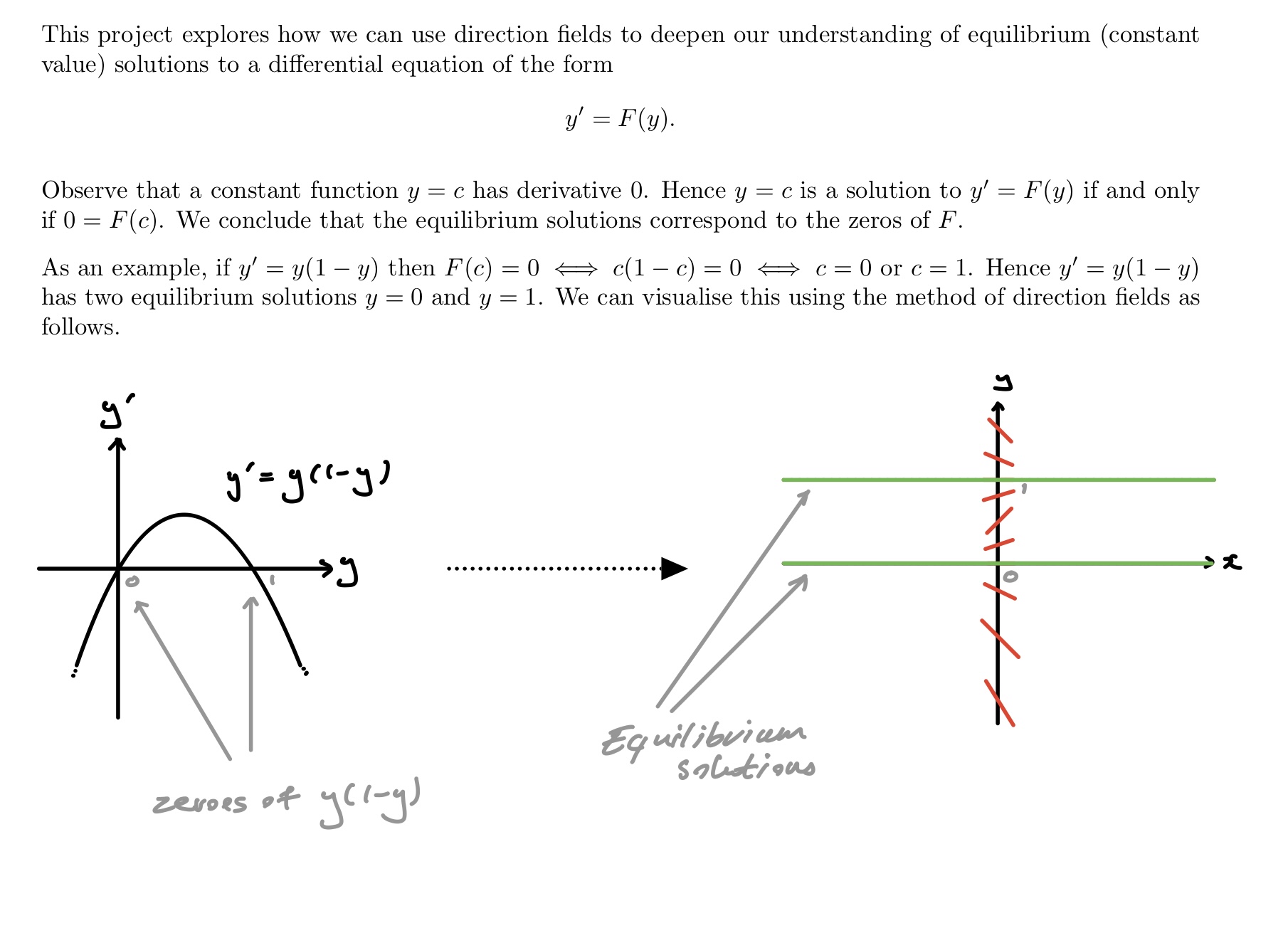
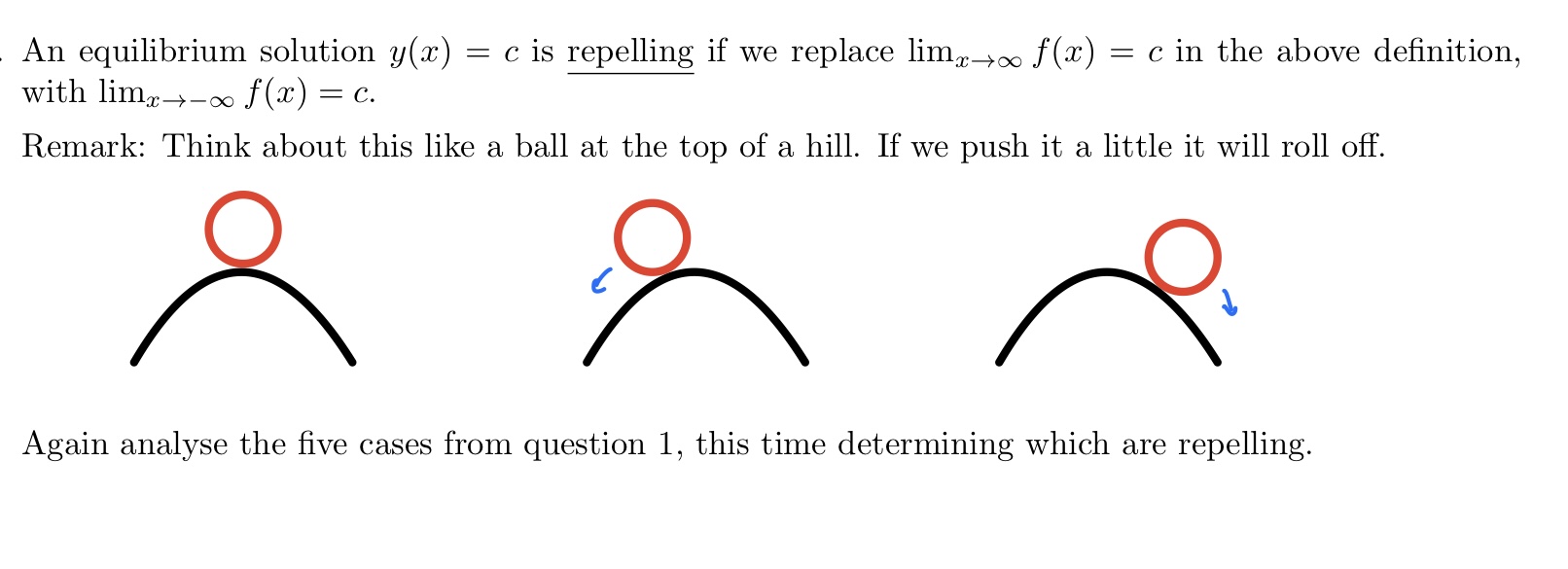
This project explores how we can use direction fields to deepen our understanding of equilibrium (constant value) solutions to a differential equation of the form y' = F(y). Observe that a constant function y = c has derivative 0. Hence y = c is a solution to y' = F(y) if and only if 0 = F(c). We conclude that the equilibrium solutions correspond to the zeros of F. As an example, if y' = y(1 - y) then F(c) = 0 c(1 -c) = 0 c = 0 or c=1. Hence y' = y(1 -y) has two equilibrium solutions y = 0 and y = 1. We can visualise this using the method of direction fields as follows. . . . . . . ......... Equilibrium solutions zeroes of y(1-g )An equilibrium solution y(x) = c is repelling if we replace limx-> f(x) = c in the above definition, with limx-- f(x) = c. Remark: Think about this like a ball at the top of a hill. If we push it a little it will roll off. Again analyse the five cases from question 1, this time determining which are repelling