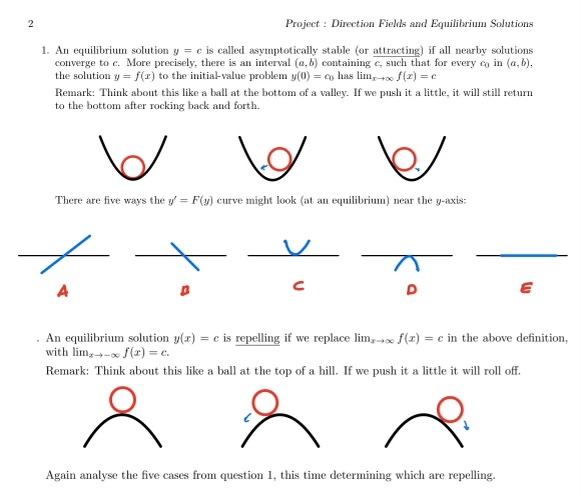
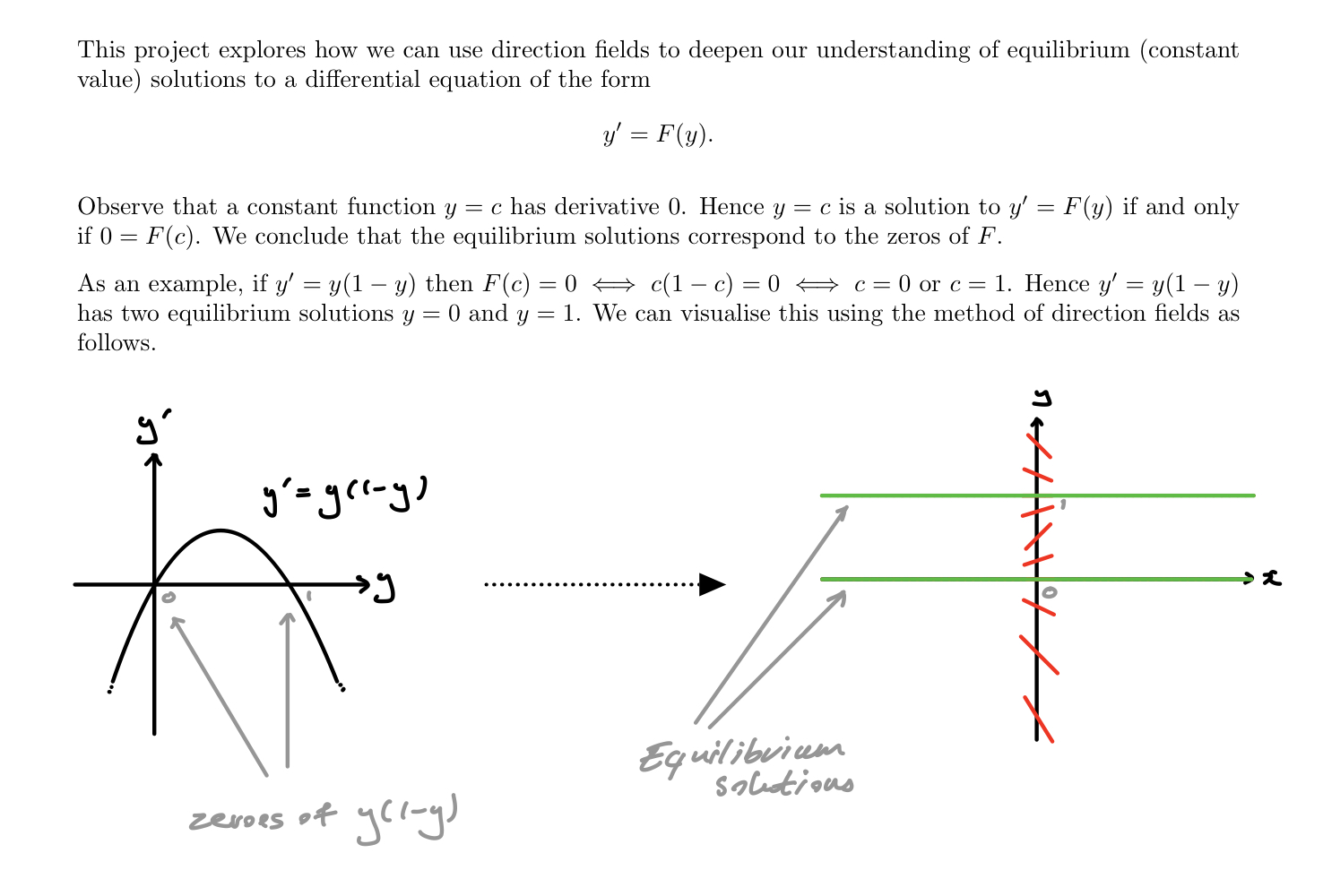
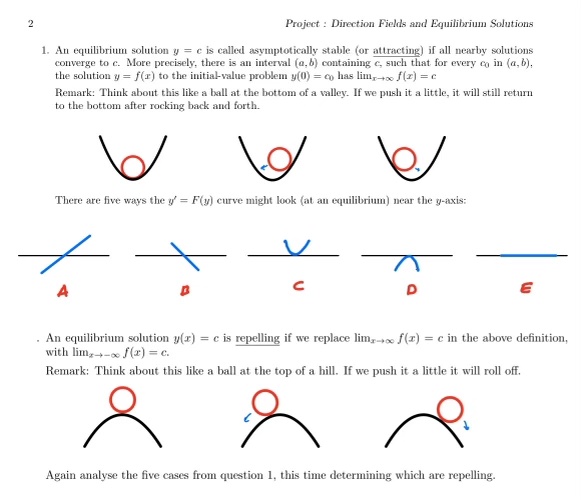
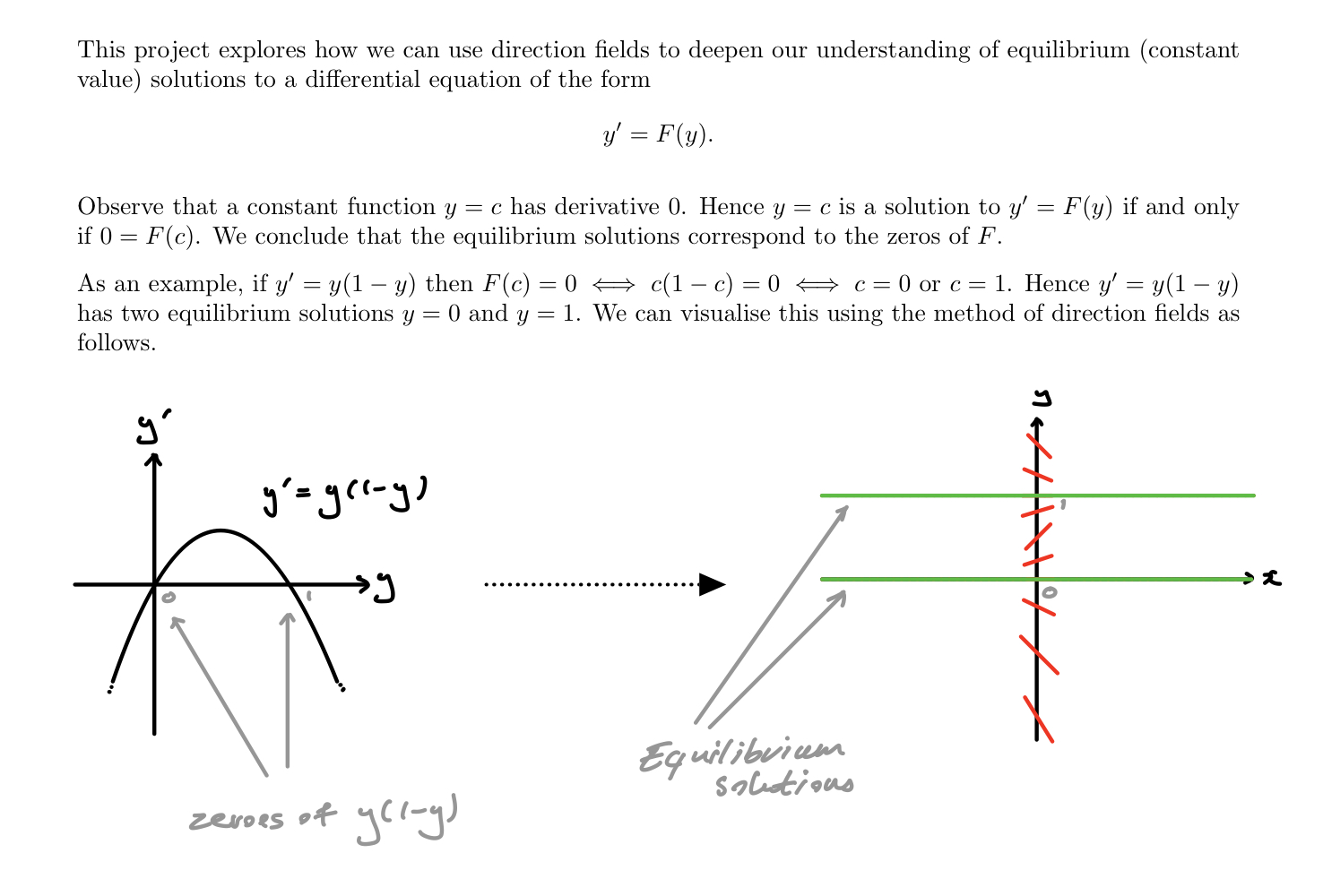
Project : Direction Fields and Equilibrium Solutions 1. An equilibrium solution y = c is called asymptotically stable (or attracting) if all nearby solutions converge to c. More precisely, there is an interval (a, b) containing e, such that for every co in (a, b), the solution y = (r) to the initial-value problem y(0) = co has lim, + /(x) = c Remark: Think about this like a ball at the bottom of a valley. If we push it a little, it will still return to the bottom after rocking back and forth. There are five ways the y' = F(y) curve might look (at an equilibrium) near the y-axis: C . An equilibrium solution y(x) = c is repelling if we replace lim,-+ /(x) = c in the above definition, with lime-+-c / (x) = c. Remark: Think about this like a ball at the top of a hill. If we push it a little it will roll off. Again analyse the five cases from question 1, this time determining which are repelling.This project explores how we can use direction elds to deepen our understanding of equilibrium (constant value) solutions to a differential equation of the form Observe that a constant function y = c has derivative 0. Hence y = c is a solution to y' = F(y) if and only if 0 : F(c) We conclude that the equilibrium solutions correspond to the zeros of F. As an example, if y' : y(1 y) then F(c) : 0 C(l c) : U <:> c : D or c : 1. Hence y' : y(1 3;) has two equilibrium solutions y : U and y : 1. We can visualise this using the method of direction elds as follows. .'3