This question contain several parts. Please write this in python codesplease use actual python file to write this which you can test them and make a screenshot about the code without write them in txt filethank you

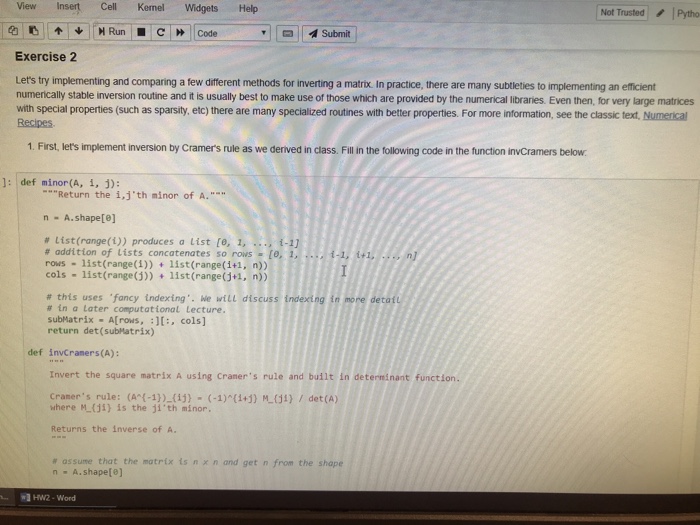
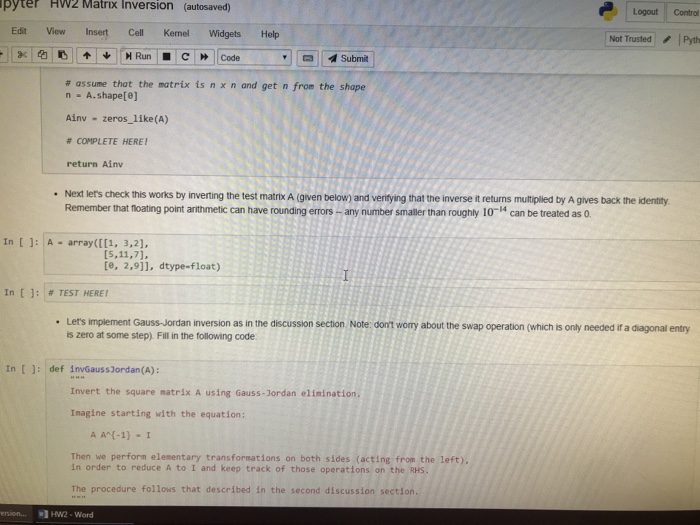
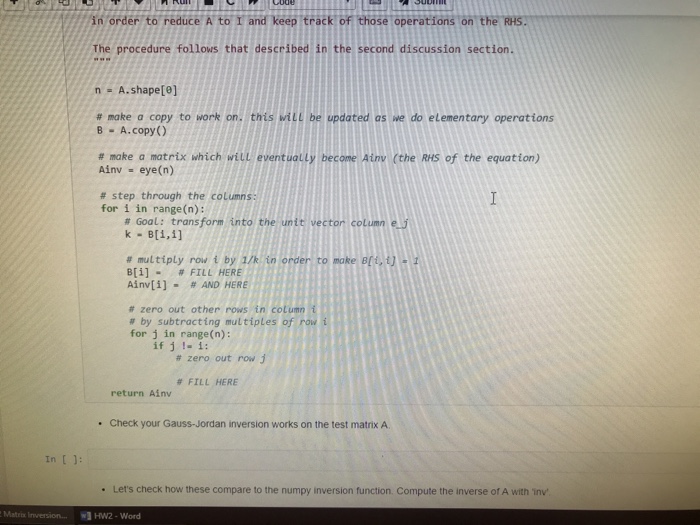
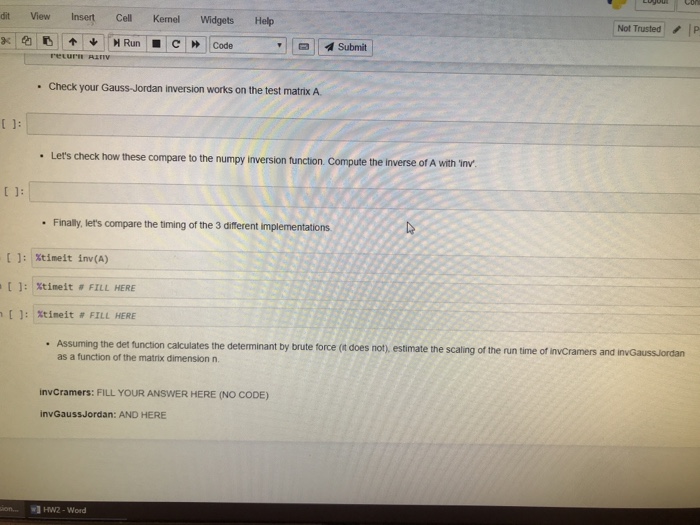
View Insert Cell Kemel WidgetsHelp Not TrustedPytho | | Submit | Exercise 2 Let's try implementing and comparing a few different methods for inverting a matrix. In practice, there are many subtleties to implementing an efficient numerically stable inversion routine and it is usually best to make use of those which are provided by the numerical libraries. Even then, for very large matrices with special properties (such as sparsity, etc) there are many specialized routines with better properties. For more information, see the classic text, Numerical Recipes 1. First, let's implement inversion by Cramer's rule as we derived in class. Fill in the following code in the function invcramers below ]: def minor(A, i, j): Return the i,j'th minor of A. n - A.shape[] # list (range()) produces a list [e, 1, # addition of lists concatenates so rows-[e, 1, ,. rows list(range(1))list(range(i+1, n)) cols list(range(list(range(j+1, n)) # this uses 'fancy indexing.. we will discuss # in a later computational Lecture. subMatrix -A[rows, :, cols] return det (subMatrix) ng in more detaft def invCraners (A): Invert the square matrix A using Crer's rule and built in determinant function Cranen's rule: (A1) (ij (1)i+) M(i) / det(A) where M(ji) is the ji'th minor Returns the inverse of A. # assume that the matrix is n n and get n from the shape n - A.shape[e] HW2-Word