This question is a assignment of Linear Algebra, especially about "Singular value decomposition". Professor said "AA^T's eigenvectors are column vectors of U matrix", but I'm not sure that should I use this. sigma is an r x r diagonal matrix whose diagonal entries are the nonzero singular values. V is a matrix that's column vectors are eigenvector of A. Following picture is about U matrix.

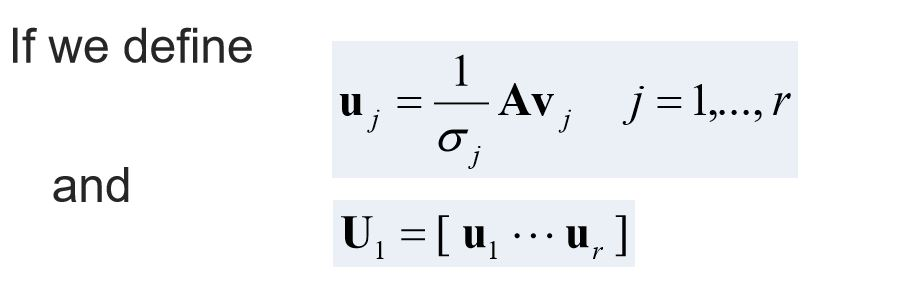
If we define 1 = Av; j = 1,..., 1 oj and U. =[u u, ] 1 For a 4x3 matrix A with columns (1,0,0,1), (0,1,0,0), and (1,0,1,-1), (a) Eigenvalues of ATA are 3, 2, 1 and their corresponding eigenvectors are (0,0,1), (1,0,0), and (0,1,0), respectively. Find an orthonormal basis of AAT, which may form the matrix U such that A = UEVT. If we define 1 = Av; j = 1,..., 1 oj and U. =[u u, ] 1 For a 4x3 matrix A with columns (1,0,0,1), (0,1,0,0), and (1,0,1,-1), (a) Eigenvalues of ATA are 3, 2, 1 and their corresponding eigenvectors are (0,0,1), (1,0,0), and (0,1,0), respectively. Find an orthonormal basis of AAT, which may form the matrix U such that A = UEVT