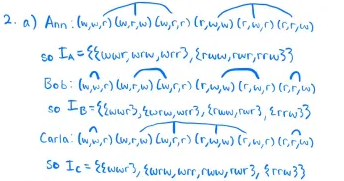
This question is about game theory class, its difficult. Please be sure you can handle it^

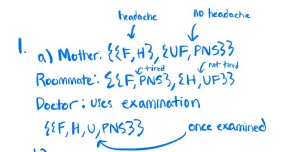
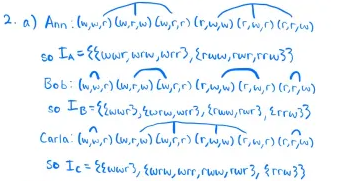
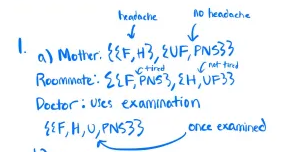
1. . You look awful: dark circles under your eyes, hanging chin, absent look, ... You must have one of the following: Flu (F): symptoms are tiredness and a headache. Hangover (H): symptoms are headache and dizziness. Unprepared for Final Syndrome (UF): symptoms are dizziness, trembling. . Prepared but no Sleep Syndrome (PNS): symptoms are trembling, tiredness. These are the only possibilities and it is well known to everybody what symptoms go with what form of sickness. It is also known that (1) you always tell your mother whether or not you have a headache, (2) you always tell your roommate whether or not you are tired and (3) you have been examined by your doctor who can always determine with absolute accuracy what your sickness is. (a) Represent what each individual (mother, roommate and doctor) knows by means of information partitions. (b) Let E be event that you either have the either flu or a hangover. Find the events "Your mother knows E", Your roommate knows E" and "Your doctor knows E". (c) Suppose that you have the flu. Does your mother know that you have the flu? Does your roommate know? Does your doctor know? (d) Let S be the event that you have either For H or UF. Find the events KS (your mother knows S). K KS (the doctor knows that your mother knows S ) and K KraS (your roommate know that your mother knows S).Q1 1 4 Points Consider question 1 from the homework. Notation: given a set of states S = {a, b, c}, an example of an information partition for individual is li = {{a, b}, {c} }, which means that if the true state is a (or b), individual I knows that the true state is either a or b; and if the true state is c, she knows this. Q1.1 1(a) 1 Point In the homework, you are asked to represent what your mother, roommate, and doctor know by means of information partitions. Which of the following partitions does not represent the knowledge of any of them? Select all that apply. OKF, PNS}, {H, UF}} O RF, H}, {UF}, { PNS}} O RF, UF} , { H, PNS}} O {{F, H}, {UF, PNS}} OUF} {H} {UF), { PNS}} O {F, H, UF, PNS}Q1.2 1(b) 1 Point Let E be the event that you either have the flu or a hangover, and A the knowledge operator for individual z. OK mother E = Kdoctor E = {F, H}, and Kroommate E = Q OK mother E = O, Kdoctor E = {F}, and KroommateE = { F, H } OK mother E = Kroommate E = , and K doctor E = {F} OK mother E = KroommateE = {F, H}, and Kdoctor E = {F}Q1.3 1(c) 1 Point Suppose you have the flu. Who knows that you have the flu? (U Your mother and the doctor, but not your roommate. (U The three of them know that you have the flu. (_) Your mother, but not your roommate nor the doctor. (O None of them knows that you have the flu. (0 The doctor, but not your mother nor your roommate. Q1.4 1(d) 1 Point Let S be the event that you have either For H or UF. O None of the above. OK mother S = {F, H}, Kdoctor Kmother S = {F, H}, and Kroommate K mother S = Q OK mother S = {F, H, UF}, K doctor Kmother S = {F, H, UF}, and K roommate K mother S = {H, UF} OK mother S = {F, H, UF}, K doctor Kmother S = {F, H, UF}, and Kroommate K mother S = {H, UF}2. Ann, Bob and Carla are taken to a room where there 15 a tray with two white balls and two red balls. Thus it becomes common knowledge among them that there are four balls, two of which are white and two are red. Then they leave the room. A referee then leads Ann to the room and asks her to pick one ball and hide it in her pocket. Then 1t becomes Bob's turn to enter the room and pick one of the remaining balls and put 1t in his pocket. Finally, Carla enters the room. picks one of the remaming balls and puts it in her pocket. It is commonly known among them that this 1s what happened. that is, that first Ann, then Bob, then Carla went to the room and picked a ball. Nobody gets to see the balls picked by the other two. However, they do see what balls are left on the tray when they make their own choice. (a) Using a set of states and information partitions, represent the state of knowledge of Ann, Bob and Carla (concerning who has what balls). (b) Draw the partition representing what 15 common knowledge between Ann and Bob. () Draw the partition representing what 1s common knowledge between Bob and Carla. (d) What strategy should Bob use i picking his ball if he wants to prevent Carla from knowing what color ball Ann has? And what 1f he wants to prevent Carla from knowing what color ball he himself has? Q2.1 2(a) 1 Point Notation: For this problem, an example of a state can be represented as {wrw}, which we will interpret as "Ann has a white ball, Bob has a red ball, and Carla has a white ball" (so the first entry corresponds to Ann, the second to Bob and the third to Carla). Which of the following is/are true with respect to the information partitions of Ann, Bob, and Carla? Select all that apply. ICarla = {wur}, {wrw, rww, rur, wrr}, {row} } I Ann = {{wwr, wrw, wrr}, {rrw, rur, rww} } ICarla = {wur}, {wrw, rww}rur, wrr}, {rrw} } IBob = {wur}, {wrw, wrr}rww, rur}, {rrw} } IAnn = {wur, wrw, wer, rrw, rur, rww} }Q2.2 2(b) 1 Point Which partition represents the common knowledge between Ann and Bob? Ofwwr, wrw, urr, rrw, rur, rww}} O {{wur, wrw, urr}, {row, rur, rww} } O {wur}, {wrw, wrr}rww, rur}, {row} } O {{wwr, wrw}, {wrr, row}, {rur, rww}}Q2.3 2(c) 1 Point Which partition represents the common knowledge between Bob and Carla? Offwur}, {wrw, wrr}, {rww, rur}, {rrw}} Ofwur}, {wrw, rww, rur, wry} {row}} Ofwwr, wrw, wrr}, row, rur, rww}} Offwur}, {wrw}, furr} {row} {rur} {rww}}Q2.4 2(d).1 0.5 Points What strategy should Bob use in picking his ball if he wants to prevent Carla from knowing what color ball Ann has?To prevent Carla from knowing what color ball Ann has: ) If Ann chooses a red ball, choose a red ball, and if Ann chooses a white ball, choose a white ball. (L) Choose either a red ball or a white ball. ! Choose a white ball. (U Choose a red ball. (_) If Ann chooses a red ball, choose a white ball, and if Ann chooses a white ball, choose a red ball. Q2.5 2(d).2 0.5 Points And what if he wants to prevent Carla from knowing what color ball he himself has? To prevent Carla from knowing what color ball he has: (U If Ann chooses a red ball, choose a white ball, and if Ann chooses a white ball, choose a red ball. (U Choose either a red ball or a white ball. (O If Ann chooses a red ball, choose a red ball, and if Ann chooses a white ball, choose a white ball. (0 Choose a white ball. (0 Choose a red ball. headache no headache ". a) Mother: (2F, H3, ZUF, PNS3 3 chind Roommate: ELF, PN53, EH, UF 3 3 Doctor: Uses examination SEF, H, U, PNS3 3 once examinedd) S = 2F, H, UF 3 Kimother S = EF, H3 ( remove UF since ZUF, PNS) , drew, rur, row3) Bob: ( w,wr) (w,r,w) (w,r,r) (r,w,w) (r,w,r) (or,w) so IB = ( Ewwr 3, Ewrw, wirr 3, Erww, For ], Errw 3 3 A Carla! ( w,w, r) (w, r,w) (w, r,r) (r,w, w) (r,w, r) (or,w) So Ic = (Ewwr], turn, war, rww, rwr 3, { row 3 3d) To prevent Carla from knowing Ann's color ball: Bodo picks diff. coker from Ann (white sred, red a white) To prevent Carla from knowing Bob's color ball: Same strategy as above