This question is provided with full information and data. Nothing is missing. Please answer it if it is possible, if you do not want to answer it, then it is ok, but do not comment this question is incomplete (this is not responsible.)

Question 3. [30 points] (Bayesian game) Consider the Bayesian game represented by the following table.

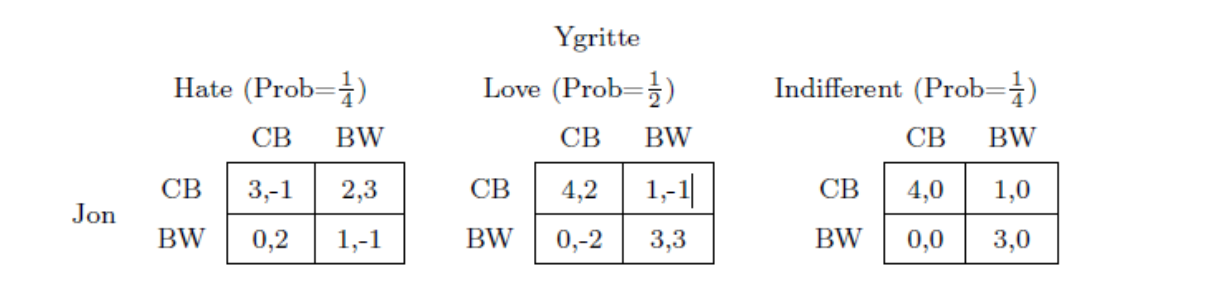
\fQuestion 3. [30 points] (Bayesian game) Consider the Bayesian game represented by the following table. Ygritte Hate (Prob=1) Love (Prob=) Indifferent (Prob=) CB BW CB BW CB BW CB 3.-1 2.3 CB 4.2 1.-1 CB 1.0 1.0 Jon BW 0.2 1.-1 BW 0.-2 3.3 BW 3.0 There are three different states: i) Ygritte hates Jon with prior probability 1/4 ii) Ygritte loves Jon with prior probability 1/2 and iii) Ygritte is indifferent for Jon with probability 1/4 . Suppose Ygritte knows her attitude perfectly. However, Jon is only fully informed if Ygritte hates him but cannot tell whether Ygritte loves him or is indifferent. 1. [4 points] How many different signals could Jon receive and how many different signals could Ygritte receive? Please write down both players' signal set and signal function. 2. [3 points] Suppose Jon receives a signal that tells him either state Love or state Indifferent will be played. Using Bayes rule calculate Jon's belief about the probability of state Love after he receives such a signal. 3. [6 points] What are Jon and Ygritte's pure strategy sets respectively? (Hint: a player's strategy in Bayesian game is a plan of actions for each signal/type.) 4. [10 points] For each possible pure strategy taken by Ygritte, please calculate Jon's expected payoffs of each of his pure strategy when he receives a signal that tells him either state Love or state Indifferent will be played 2 5. [7 points] Find the set of all pure strategy Nash Equilibria of this game