This Questions have two man Parts ( Case a , Case b). Three pictures are attached here. Pictures aa attached for concept and picture bb and Picture cc have questions and its parts.

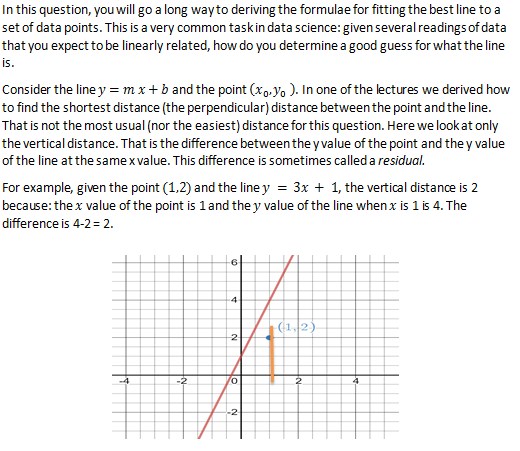
In this question, you will go a long way to deriving the formulae for fitting the best line to a set of data points. This is a very common task in data science: given several readings of data that you expect to be linearly related, how do you determine a good guess for what the line is. Consider the line y = m x + b and the point (x, y, ). In one of the lectures we derived how to find the shortest distance (the perpendicular) distance between the point and the line. That is not the most usual (nor the easiest) distance for this question. Here we look at only the vertical distance. That is the difference between the yvalue of the point and the y value of the line at the same x value. This difference is sometimes called a residual. For example, given the point (1,2) and the liney = 3x + 1, the vertical distance is 2 because: the x value of the point is 1 and the y value of the line when x is 1 is 4. The difference is 4-2 = 2. 2. (12) -2 2The length of the green vertical line is 2. a. Specific Case: You have done three experiments, leading to the following three results correlating the xvalue and the y value: (1,2); (2,4); (3,5). We are going to fit a line to the data as follows: we will find the line that minimises the sum of the squares of the residuals between these points and the line. We use the square partially because the square is always positive, so we do not have to worry about signs. It is much easier to work with squares than with absolute values. i. Consider the liney = m x + b and the point (X,.yo ). Find an expression for the vertical distance between the line and the point; i.e. the residual. ii. Now assume we have a line y = m x + b,and the points above, what are the three residuals. Note that your answers will have m's and b's in them. iii. The function D(m. b), represents the sum of the squares of the residuals: ie. You square each residual and add the results. Write a formula for D (m, b). iv. Optimise D(m. b) by taking the partial derivative with respect to each of the two variables and setting them equal to zero. This will lead to two linear equations in two unknowns. V. Solve the equations to find the values of m and b vi. Draw a graph with the three points and the line to make sure it looks reasonable. If not: gotoii. vii. Check your answer by going to the Wolfram Alpha website and typing: 'best fit line (1,2), (2,4), (3,5)'. If you have the wrong answer: goto ii.b. General case. Do exactly what you did above but instead of the three specific points, use k points with unknown values: (Xo.Vo )(x.V ).... (Xk-1.)k-1 ) i. Again, the function D(m.b), represents the sum of the squares of the residuals. Write a formula for D (m, b). It is easier now, and will be much easier in the next part, if you work with these quantities using sigmanotation. For example, write the sum XotX,to+Xx-1 as Exi ii. We will optimise (m. b) . Take the partial derivative with respect to each of the two variables and setting them equal to zero. This, again, will lead to two linear equations in two unknowns. Note that it is very important that we think of the (x y) points as constants, even though we do not know their values. iii. Solve the two equations to the extent that they are each written in the form: b = a fraction that involes a m.x. yuck and preferably Sigma signs Note that it may not be that both equations use all the symbols iv. Use your equations in iii to find the equation of the best-fit line to the following data: (1,2); (1,3), (2,4), (2,2), (4,8), (3,5), (4.5) When you plug in the data, you should end up with two linear equations in two unknowns v. (for the Algebraically intrepid) Manipulate your equations in iii to end up with one of the standard equations for linear regression. Take your two equations of the form b = something and set the two somethings equal to each other. Cross multiply and manipulate