THRD Question

(20 points) A financial advisor wants to maximize a portfolio consisting of 2 stocks, X and Y. However, the risk calculations are complex and involve nonlinear formulations. In particular, the problem to be solved is as follows:

Maximize portfolio return = (5%)X+(7%)Y

Subject to:

3X + 2X2 + 4Y +3/Y

5X + 6XY

4X + Y

X, Y >=0

Solve this problem using Excel i) starting from the initial point (1,1), ii) starting from the initial

point (20,2). What happens in each case? Report on your observations regarding the

solution.

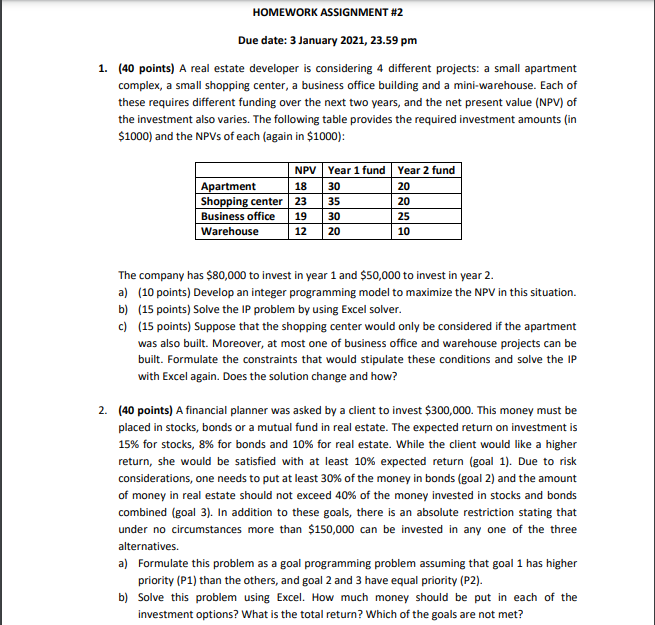
HOMEWORK ASSIGNMENT #2 Due date: 3 January 2021, 23.59 pm 1. (40 points) A real estate developer is considering 4 different projects: a small apartment complex, a small shopping center, a business office building and a mini-warehouse. Each of these requires different funding over the next two years, and the net present value (NPV) of the investment also varies. The following table provides the required investment amounts (in $1000) and the NPVS of each (again in $1000): NPV Year 1 fund Year 2 fund Apartment 18 30 20 Shopping center 23 35 20 Business office 19 30 Warehouse 12 20 10 25 The company has $80,000 to invest in year 1 and $50,000 to invest in year 2. a) (10 points) Develop an integer programming model to maximize the NPV in this situation. b) (15 points) Solve the IP problem by using Excel solver. c) (15 points) Suppose that the shopping center would only be considered if the apartment was also built. Moreover, at most one of business office and warehouse projects can be built. Formulate the constraints that would stipulate these conditions and solve the IP with Excel again. Does the solution change and how? 2. (40 points) A financial planner was asked by a client to invest $300,000. This money must be placed in stocks, bonds or a mutual fund in real estate. The expected return on investment is 15% for stocks, 8% for bonds and 10% for real estate. While the client would like a higher return, she would be satisfied with at least 10% expected return (goal 1). Due to risk considerations, one needs to put at least 30% of the money in bonds (goal 2) and the amount of money in real estate should not exceed 40% of the money invested in stocks and bonds combined (goal 3). In addition to these goals, there is an absolute restriction stating that under no circumstances more than $150,000 can be invested in any one of the three alternatives. a) Formulate this problem as a goal programming problem assuming that goal 1 has higher priority (P1) than the others, and goal 2 and 3 have equal priority (P2). b) Solve this problem using Excel. How much money should be put in each of the investment options? What is the total return? Which of the goals are not met? HOMEWORK ASSIGNMENT #2 Due date: 3 January 2021, 23.59 pm 1. (40 points) A real estate developer is considering 4 different projects: a small apartment complex, a small shopping center, a business office building and a mini-warehouse. Each of these requires different funding over the next two years, and the net present value (NPV) of the investment also varies. The following table provides the required investment amounts (in $1000) and the NPVS of each (again in $1000): NPV Year 1 fund Year 2 fund Apartment 18 30 20 Shopping center 23 35 20 Business office 19 30 Warehouse 12 20 10 25 The company has $80,000 to invest in year 1 and $50,000 to invest in year 2. a) (10 points) Develop an integer programming model to maximize the NPV in this situation. b) (15 points) Solve the IP problem by using Excel solver. c) (15 points) Suppose that the shopping center would only be considered if the apartment was also built. Moreover, at most one of business office and warehouse projects can be built. Formulate the constraints that would stipulate these conditions and solve the IP with Excel again. Does the solution change and how? 2. (40 points) A financial planner was asked by a client to invest $300,000. This money must be placed in stocks, bonds or a mutual fund in real estate. The expected return on investment is 15% for stocks, 8% for bonds and 10% for real estate. While the client would like a higher return, she would be satisfied with at least 10% expected return (goal 1). Due to risk considerations, one needs to put at least 30% of the money in bonds (goal 2) and the amount of money in real estate should not exceed 40% of the money invested in stocks and bonds combined (goal 3). In addition to these goals, there is an absolute restriction stating that under no circumstances more than $150,000 can be invested in any one of the three alternatives. a) Formulate this problem as a goal programming problem assuming that goal 1 has higher priority (P1) than the others, and goal 2 and 3 have equal priority (P2). b) Solve this problem using Excel. How much money should be put in each of the investment options? What is the total return? Which of the goals are not met