Question: TIP: Maximize your browser for best viewing of this problem. The graph of the rational function Ax) is shown. It has a horizontal asymptote of
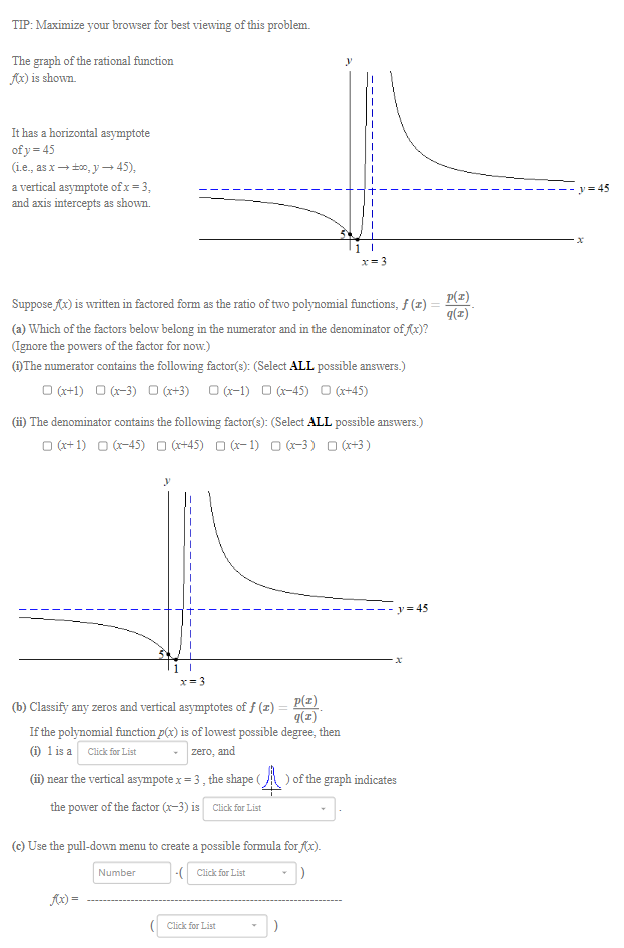
![asymptote of y = 45 (i.e., as x -+ 100, ] -+](https://s3.amazonaws.com/si.experts.images/answers/2024/06/667b37b274eab_218667b37b263743.jpg)
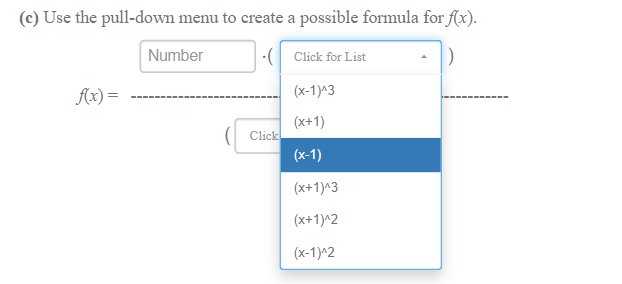
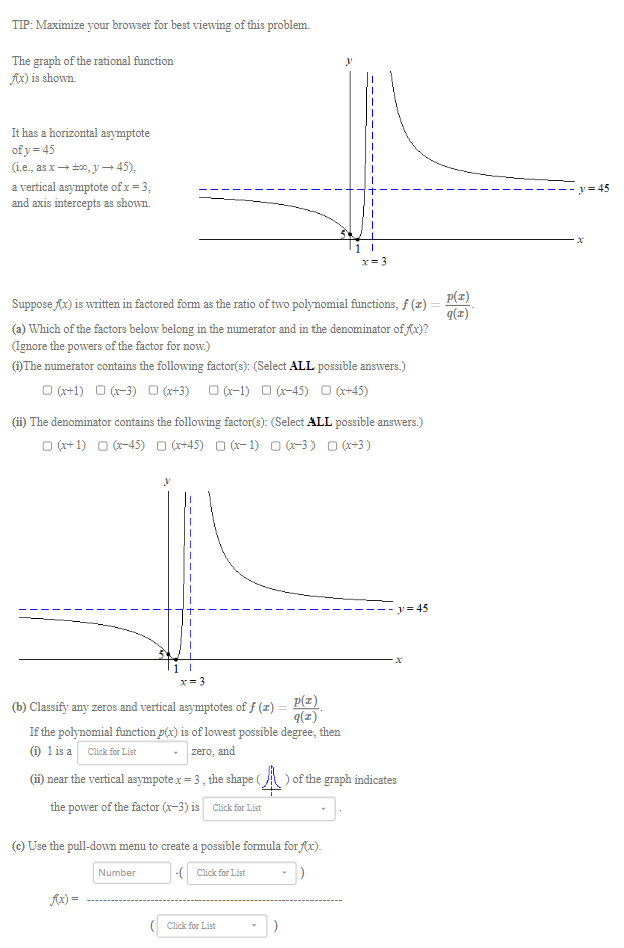
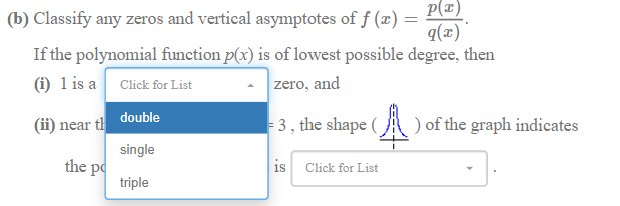
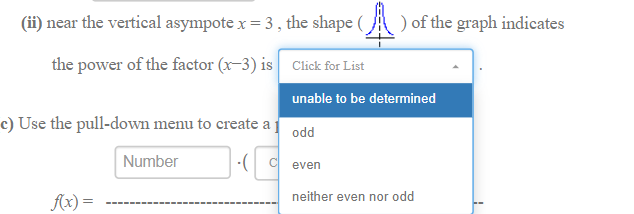
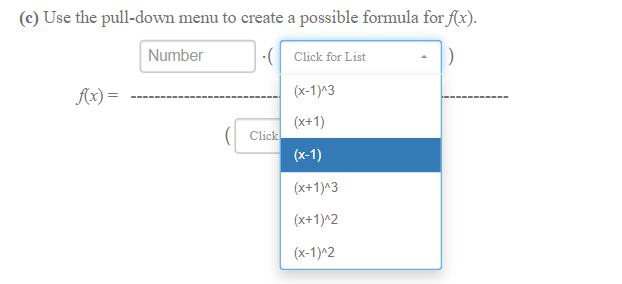
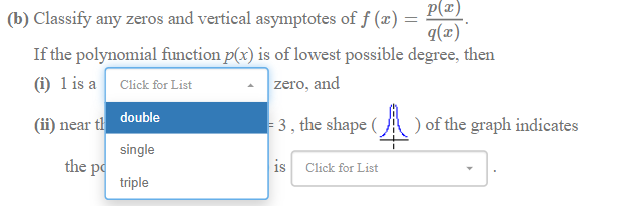
TIP: Maximize your browser for best viewing of this problem. The graph of the rational function Ax) is shown. It has a horizontal asymptote of y = 45 (i.e., as x -+ 100, ] -+ 45), a vertical asymptote of x = 3, y = 45 and axis intercepts as shown. x = 3 Suppose f(x) is written in factored form as the ratio of two polynomial functions, f (r) = P(I) q(I) (a) Which of the factors below belong in the numerator and in the denominator of ((x)? (Ignore the powers of the factor for now.) (i) The numerator contains the following factor(s): (Select ALL possible answers.) O (x+1) 0 (x-3) 0(+3) 0(-1) 0 (x-45) 0 (x+45) (ii) The denominator contains the following factor(s): (Select ALL possible answers.) 0 (x+1) 0 (x-45) 0 (x+45) 0(x-1) 0(x-3) 0(x+3) - - 1 = 45 x = 3 (b) Classify any zeros and vertical asymptotes of f (I) = P _P(I) q(I) If the polynomial function p(x) is of lowest possible degree, then (i) 1 is a Click for List zero, and (ii) near the vertical asympote x = 3 , the shape (_/ \\ ) of the graph indicates the power of the factor (x-3) is Click for List (c) Use the pull-down menu to create a possible formula for f(x). Number - ( Click for List Ax) = Click for List(b) Classify any zeros and vertical asymptotes of f (x) = P(I) q(x) If the polynomial function p(x) is of lowest possible degree, then (i) 1 is a Click for List zero, and (ii) near th double 3 , the shape ) of the graph indicates single the po Click for List triple(ii) near the vertical asympote x = 3 , the shape ( ) of the graph indicates the power of the factor (x-3) is Click for List unable to be determined c) Use the pull-down menu to create a odd Number C even A(x) = neither even nor odd(c) Use the pull-down menu to create a possible formula for f(x). Number Click for List Ax) = (x-1)^3 (x+1) Click (x-1) (x+1)^3 (x+1)^2 (x-1)^2
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


