Transition Probability

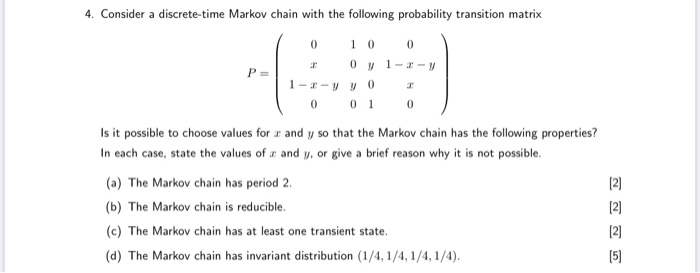
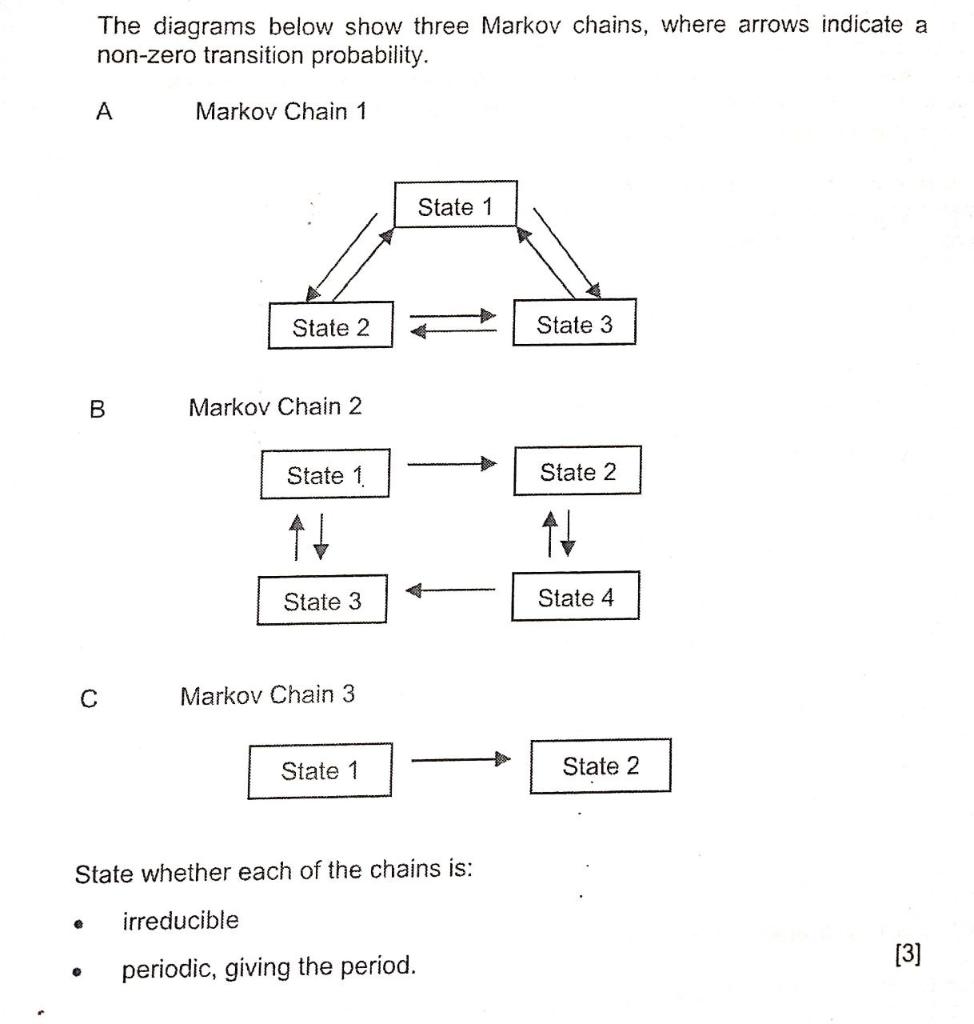
A Markov chain with state space {1, 2, 3} has transition probability matrix 0.6 0.3 0.1\\ P. = 0.3 0.3 0.4 0.4 0.1 0.5 (a) Is this Markov chain irreducible? Is the Markov chain recurrent or transient? Explain your answers. (b) What is the period of state 1? Hence deduce the period of the remaining states. Does this Markov chain have a limiting distribution? (c) Consider a general three-state Markov chain with transition matrix P11 P12 P13 P = P21 P22 P23 P31 P32 P33 Give an example of a specific set of probabilities p;; for which the Markov chain is not irreducible (there is no single right answer to this, of course !).4. Consider a discrete-time Markov chain with the following probability transition matrix 0 0 0 0 7 1-3-y P = 1-I-VVO T 0 0 1 0 Is it possible to choose values for a and y so that the Markov chain has the following properties? In each case, state the values of a and y, or give a brief reason why it is not possible. (a) The Markov chain has period 2. [2) (b) The Markov chain is reducible. (c) The Markov chain has at least one transient state. UNN (d) The Markov chain has invariant distribution (1/4, 1/4, 1/4, 1/4).The diagrams below show three Markov chains, where arrows indicate a non-zero transition probability. A Markov Chain 1 State 1 State 2 State 3 B Markov Chain 2 State 1 State 2 State 3 State 4 C Markov Chain 3 State 1 State 2 State whether each of the chains is: e irreducible . periodic, giving the period. [3]