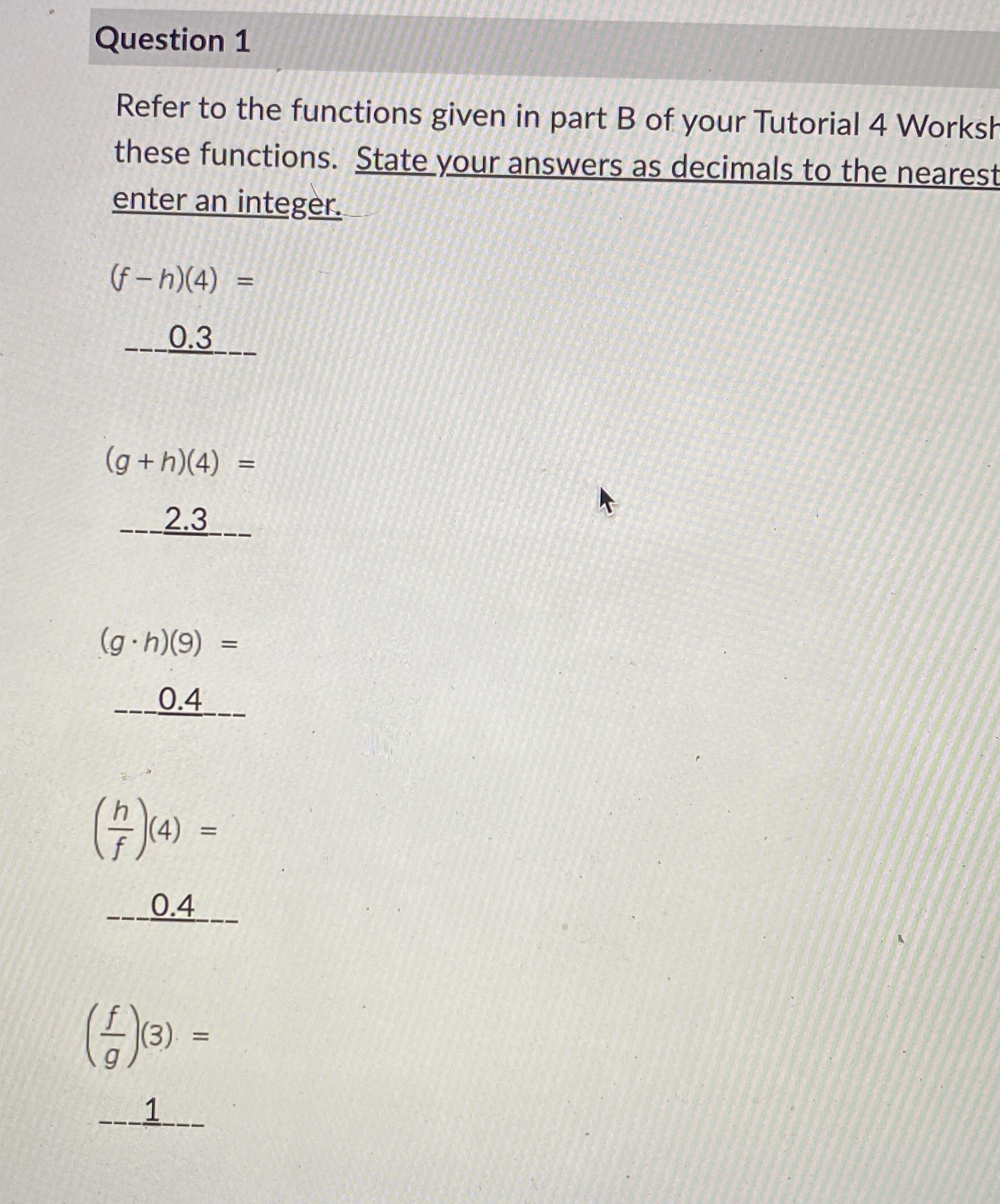
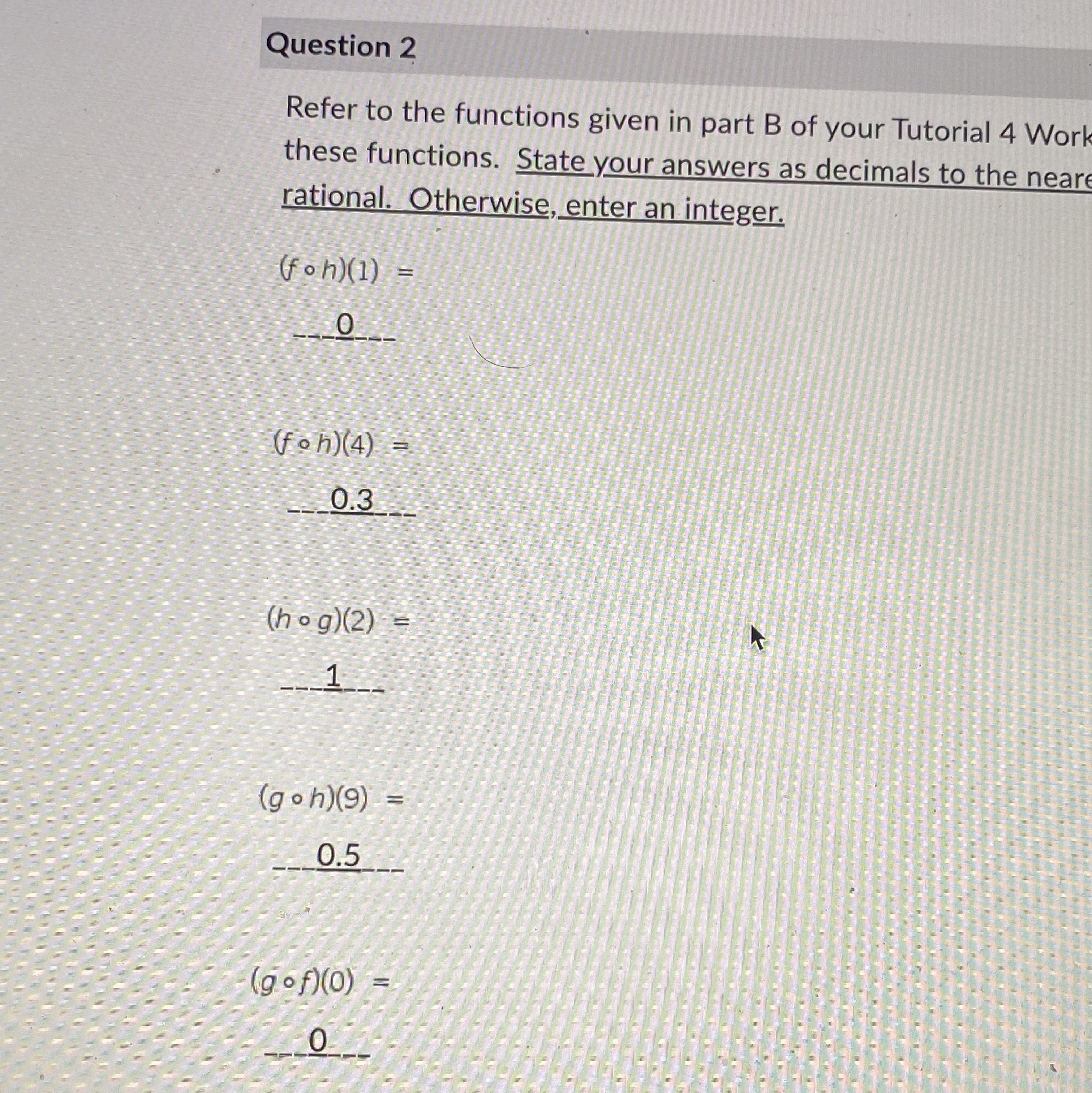
Tutorial 4 Combinations, Compositions, and Inverse Functions Math 0130 Given the functions, f (x) = x - 1 g(x) 1 x+1 h (x) = Vx x-1 1. Determine the following. Clearly show your work and use the correct notation.Question 1 Refer to the functions given in part B of your Tutorial 4 Worksh these functions. State your answers as decimals to the nearest enter an integer. (f - h) (4) = 0.3 (g + h)(4) = 2.3 (g . h)(9) = 0.4 0.4 -__1_ _ _Question 2 Refer to the functions given in part B of your Tutorial 4 Work these functions. State your answers as decimals to the near rational. Otherwise, enter an integer. (foh)(1) = 0 (f oh) ( 4) = 0.3 (hog)(2) 1_ (g o h)(9) = 0.5 (g of)(0) 0termine whether each of the following statements are true or false. Enter T for tru The function f(x) = x2 is invertible on its natural domain. The function f(x) = X" , x 20 is a one-to-one function and is invertible. The function f(x) =2 -v4 -X has a restricted domain. The function f(x) =2 - V4-x is not invertible. The inverse function of f(x) =2 -V4-x is f-1(x) = 2-(4-x). The inverse function of f(x) =2 -V4-x is f (x) =4-(2 -x)2 . The inverse function of f(x)=2 -V4-x is f 1(x) = 4-(2 -x)2, x52 . Functions f(x) and g(x) are inverses if (f . g)(x) = x . If the domain of a function is x 2 0 , then the range of the inverse function is v20 T