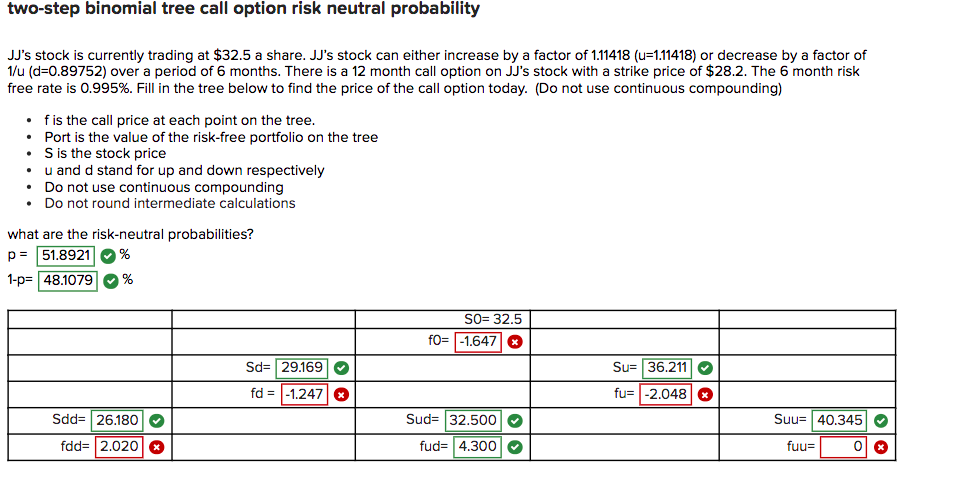
two-step binomial tree call option risk neutral probability JJ's stock is currently trading at $32.5 a share. JJ's stock can either increase by a factor of 1.11418 (u=1.11418) or decrease by a factor of 1/u (d=0.89752) over a period of 6 months. There is a 12 month call option on JJ's stock with a strike price of $28.2. The 6 month risk free rate is 0.995%. Fill in the tree below to find the price of the call option today. (Do not use continuous compounding) fis the call price at each point on the tree. Port is the value of the risk-free portfolio on the tree S is the stock price u and d stand for up and down respectively Do not use continuous compounding Do not round intermediate calculations what are the risk-neutral probabilities? p= 51.8921 % 1-p= 48.1079 % SO= 32.5 fo= -1.647| Sd= 29.169 Su= 36.211 fd = -1.247 fu= -2.048 Sdd=26180 Sud= 32.500 Suu= 40.345 fdd= 2.020 fud= 4.300 fuu 0