undefined

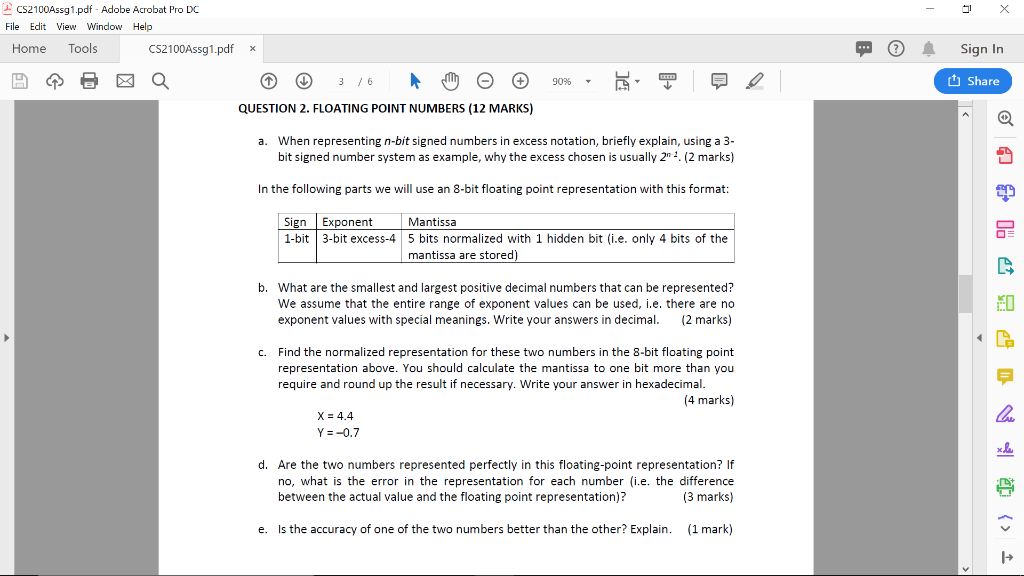
CS2100Assg1.pdf - Adobe Acrobat Pro DC File Edit View Window Help Home Tools CS2100Assg1.pdf Sign In Q 3/6 90% Share QUESTION 2. FLOATING POINT NUMBERS (12 MARKS) a. When representing n-bit signed numbers in excess notation, briefly explain, using a 3- bit signed number system as example, why the excess chosen is usually 202. (2 marks) In the following parts we will use an 8-bit floating point representation with this format: Sign Exponent Mantissa 1-bit 3-bit excess-4 5 bits normalized with 1 hidden bit (i.e. only 4 bits of the mantissa are stored) b. What are the smallest and largest positive decimal numbers that can be represented? We assume that the entire range of exponent values can be used, i.e. there are no exponent values with special meanings. Write your answers in decimal. (2 marks) PO Find the normalized representation for these two numbers in the 8-bit floating point representation above. You should calculate the mantissa to one bit more than you require and round up the result if necessary. Write your answer in hexadecimal. (4 marks) X = 4.4 Y = -0.7 6 do e O V ED > 1 d. Are the two numbers represented perfectly in this floating-point representation? If no, what is the error in the representation for each number (i.e. the difference between the actual value and the floating point representation)? (3 marks) e Is the accuracy of one of the two numbers better than the other? Explain. (1 mark) 1 CS2100Assg1.pdf - Adobe Acrobat Pro DC File Edit View Window Help Home Tools CS2100Assg1.pdf Sign In Q 3/6 90% Share QUESTION 2. FLOATING POINT NUMBERS (12 MARKS) a. When representing n-bit signed numbers in excess notation, briefly explain, using a 3- bit signed number system as example, why the excess chosen is usually 202. (2 marks) In the following parts we will use an 8-bit floating point representation with this format: Sign Exponent Mantissa 1-bit 3-bit excess-4 5 bits normalized with 1 hidden bit (i.e. only 4 bits of the mantissa are stored) b. What are the smallest and largest positive decimal numbers that can be represented? We assume that the entire range of exponent values can be used, i.e. there are no exponent values with special meanings. Write your answers in decimal. (2 marks) PO Find the normalized representation for these two numbers in the 8-bit floating point representation above. You should calculate the mantissa to one bit more than you require and round up the result if necessary. Write your answer in hexadecimal. (4 marks) X = 4.4 Y = -0.7 6 do e O V ED > 1 d. Are the two numbers represented perfectly in this floating-point representation? If no, what is the error in the representation for each number (i.e. the difference between the actual value and the floating point representation)? (3 marks) e Is the accuracy of one of the two numbers better than the other? Explain. (1 mark) 1