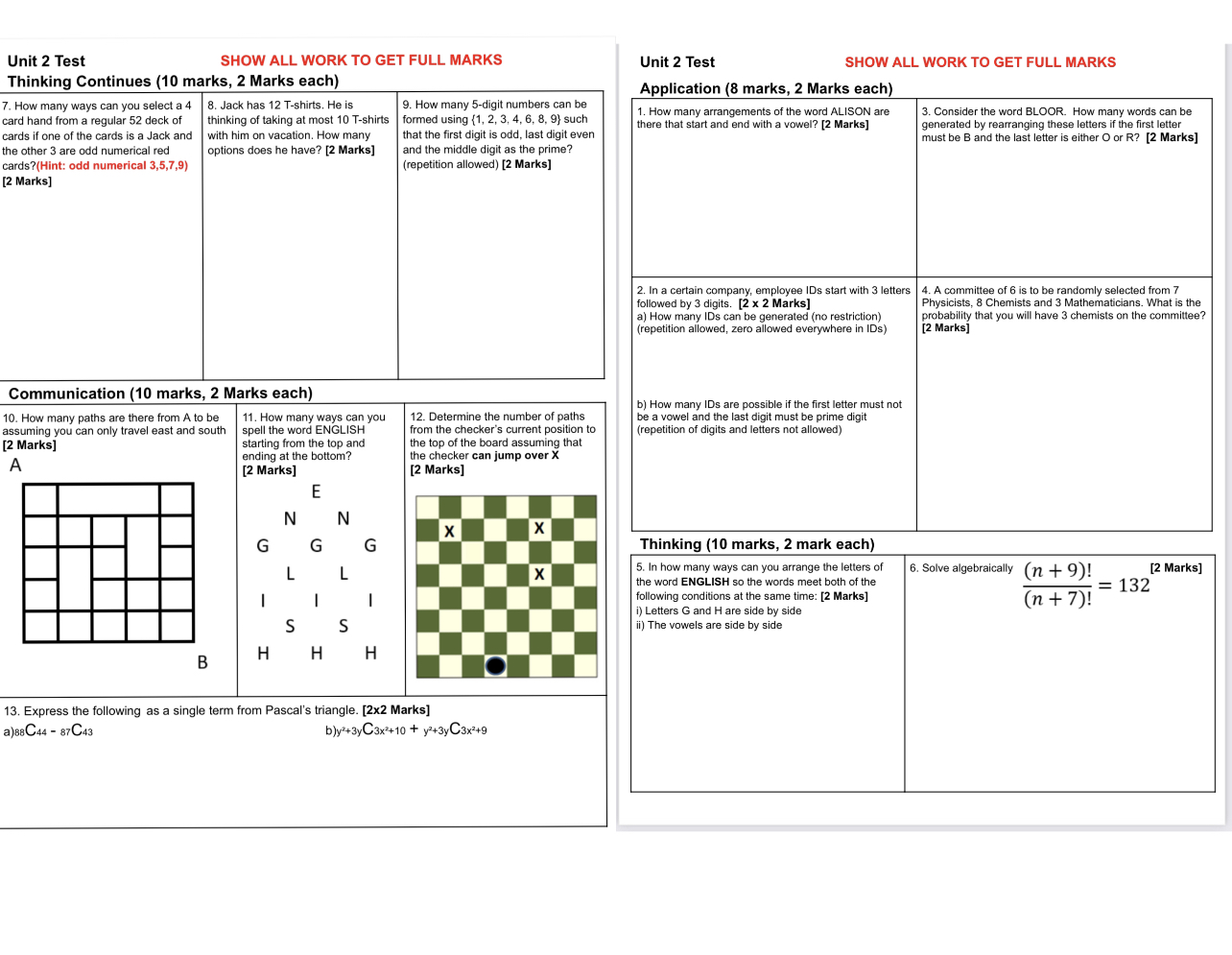
Unit 2 Test SHOW ALL WORK TO GET FULL MARKS Unit 2 Test SHOW ALL WORK TO GET FULL MARKS Thinking Continues (10 marks, 2 Marks each) Application (8 marks, 2 Marks each) 7. How many ways can you select a 4 8. Jack has 12 T-shirts. He is 9. How many 5-digit numbers can be card hand from a regular 52 deck of thinking of taking at most 10 T-shirts formed using {1, 2, 3, 4, 6, 8, 9} such 1. How many arrangements of the word ALISON are . Consider the word BLOOR. How many words can be generated by rearranging these letters if the first letter cards if one of the cards is a Jack and |with him on vacation. How many that the first digit is odd, last digit even there that start and end with a vowel? [2 Marks] must be B and the last letter is either O or R? [2 Marks] the other 3 are odd numerical red options does he have? [2 Marks] and the middle digit as the prime? cards?(Hint: odd numerical 3,5,7,9) (repetition allowed) [2 Marks] [2 Marks] 2. In a certain company, employee IDs start with 3 letters | 4. A committee of 6 is to be randomly selected from 7 followed by 3 digits. [2 x 2 Marks] Physicists, 8 Chemists and 3 Mathematicians. What is the a) How many IDs can be generated (no restriction) probability that you will have 3 chemists on the committee? (repetition allowed, zero allowed everywhere in IDs) [2 Marks] Communication (10 marks, 2 Marks each) b) How many IDs are possible if the first letter must not 10. How many paths are there from A to be 11. How many ways can you 12. Determine the number of paths be a vowel and the last digit must be prime digit assuming you can only travel east and south spell the word ENGLISH from the checker's current position to (repetition of digits and letters not allowed) [2 Marks] starting from the top and he top of the board assuming that ending at the bottom? the checker can jump over X A [2 Marks] [2 Marks] X X G Thinking (10 marks, 2 mark each) X 5. In how many ways can you arrange the letters of 6. Solve algebraically (n + 9)! [2 Marks] the word ENGLISH so the words meet both of the ollowing conditions at the same time: [2 Marks] : 132 (n + 7)! ) Letters G and H are side by side i) The vowels are side by side H H H B 13. Express the following as a single term from Pascal's triangle. [2x2 Marks] a)88C44 - 87C43 b)yz+3yC3x*+10 + yz+3yC3x3+9