upload your scripts and screenshot

Using matlab

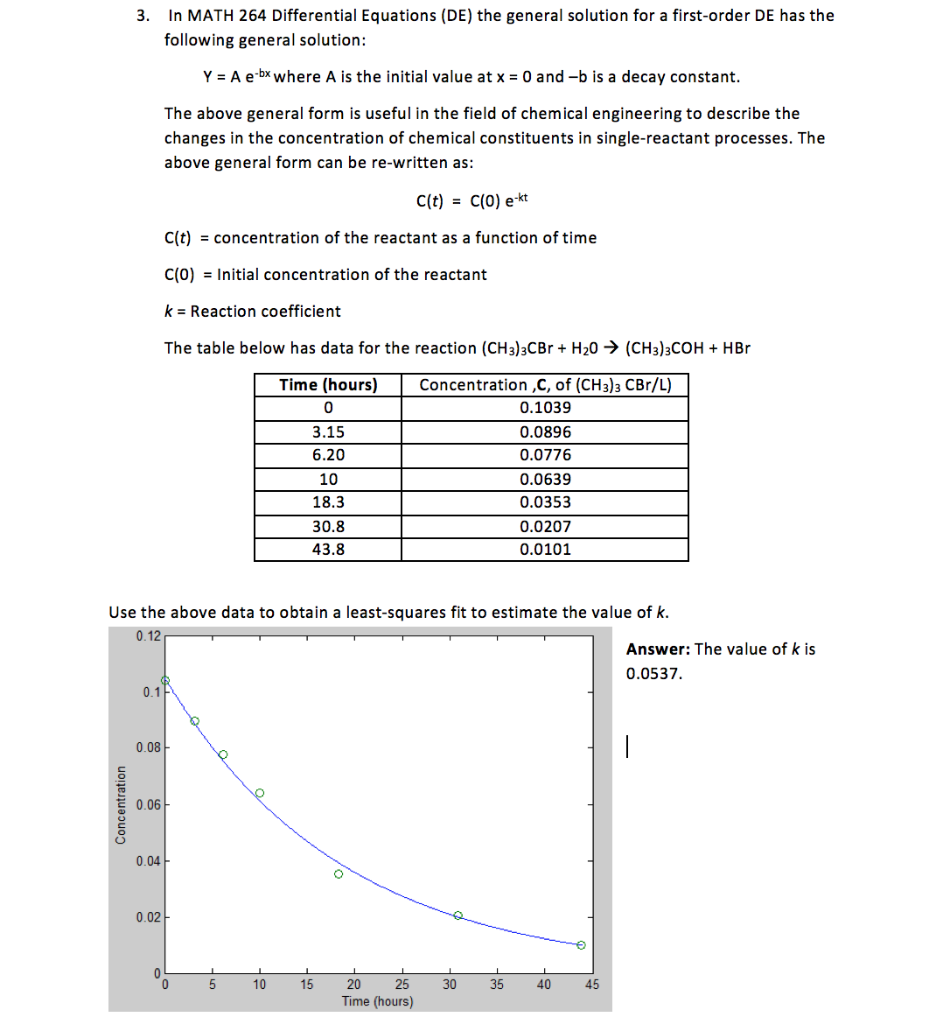
3. In MATH 264 Differential Equations (DE) the general solution for a first-order DE has the following general solution: Y = A e-bx where A is the initial value at x = 0 and -b is a decay constant. The above general form is useful in the field of chemical engineering to describe the changes in the concentration of chemical constituents in single-reactant processes. The above general form can be re-written as: C(t) = c(0) e-kt C(t) = concentration of the reactant as a function of time C(0) = Initial concentration of the reactant k = Reaction coefficient The table below has data for the reaction (CH3)3CBr + H20 (CH3)3COH + HBr Time (hours) 0 3.15 6.20 10 18.3 30.8 43.8 Concentration ,C, of (CH3)3 CBr/L) 0.1039 0.0896 0.0776 0.0639 0.0353 0.0207 0.0101 Use the above data to obtain a least-squares fit to estimate the value of k. 0.12 Answer: The value of k is 0.0537. 01R Concentration o 10 15 20 25 30 35 40 45 Time (hours)