use C++ PROVIDE SCREENSHOT ALSO and code must be type written

The Weibull Distribution is used to assess product reliability and model failure times.

We can determine if the number of failures is increasing with time, decreasing with time, or remaining constant.

The following equations are used to compute for the Weibull Distribution of a product:

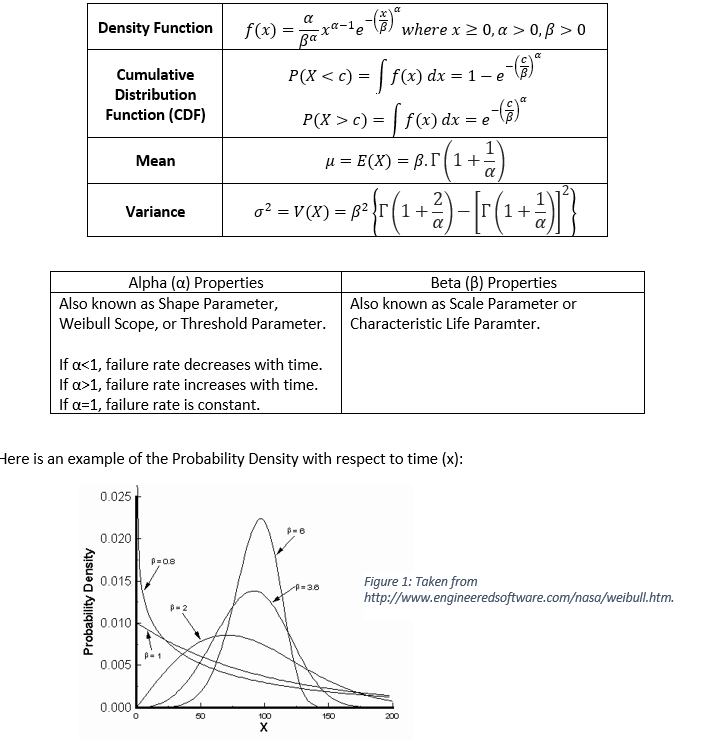
Based on Figure 1, failure rates can increase or decrease with respect to time and depending on the alpha and beta properties of the product.

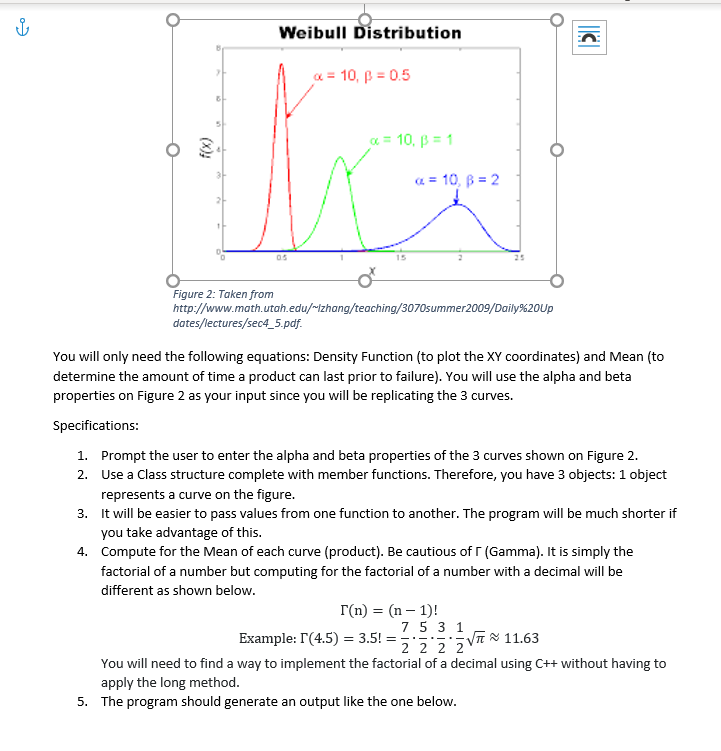
For this machine problem, create a program that will replicate the Weibull Distribution below.

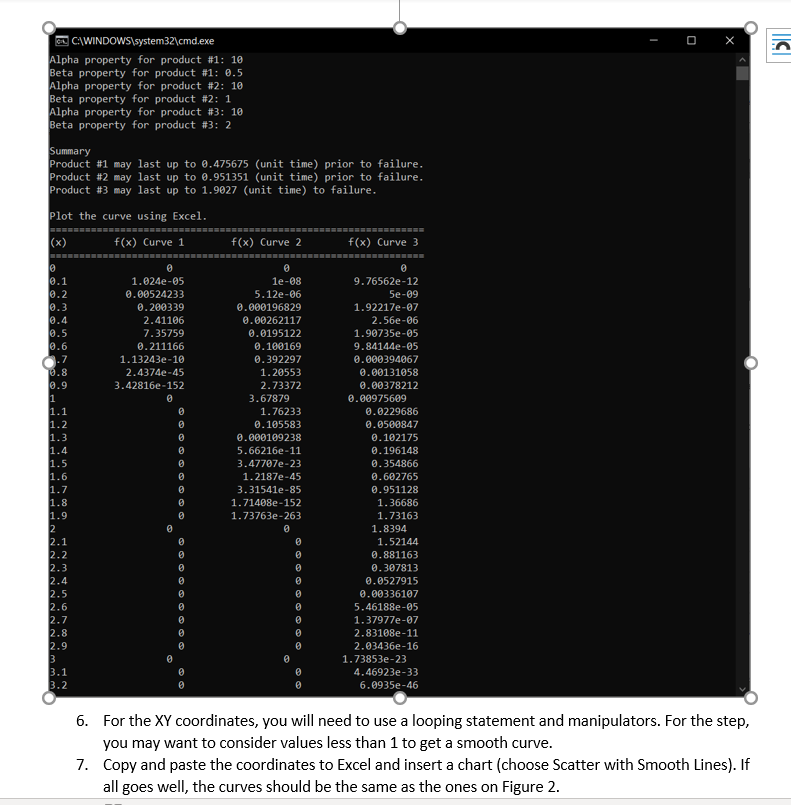
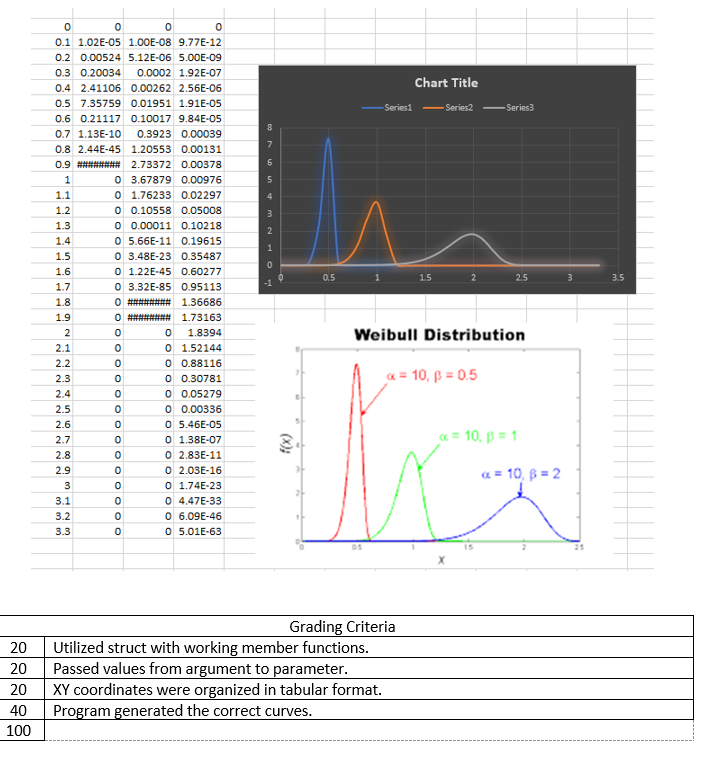
USE THIS STARTING CODE

]#include #include #include

using namespace std;

struct Weibull { double alpha; double beta; double meanResult;

Weibull(); ~Weibull(); void Density(Weibull, Weibull); void Mean(double, double); void displayResults(Weibull, Weibull); };

Weibull::Weibull() { this->alpha = 0; this->beta = 0; this->meanResult = 0; }

Weibull::~Weibull() { }

void Weibull::Density(Weibull distribution2, Weibull distribution3) { }

void Weibull::Mean(double alpha, double beta) { this->alpha = alpha; this->beta = beta; this->meanResult = beta * (tgamma(1 + 1 / alpha)); }

void Weibull::displayResults(Weibull distribution2, Weibull distribution3) { cout

int main() { Weibull distribution1, distribution2, distribution3; void assignProperties(Weibull&, double, double); double alpha, beta;

for (int x = 1; x > alpha; cout > beta;

switch (x) { case 1: assignProperties(distribution1, alpha, beta); break; case 2: assignProperties(distribution2, alpha, beta); break; case 3: assignProperties(distribution3, alpha, beta); break; } }

distribution1.displayResults(distribution2, distribution3); distribution1.Density(distribution2, distribution3);

return 0; }

void assignProperties(Weibull& distribution, double alpha, double beta) { distribution.Mean(alpha, beta);

a Density Function f(x) = =x*-1e Cumulative Distribution Function (CDF) ** where x 20, a > 0,8>0 P(X c) = {f(x) dx = e (3) 4 = B.TO ver) sr(1+3) [p(1+2) a"} Mean u = E(X) = B.1(1+ a Variance o2 = V(X) = B2 Alpha (a) Properties Also known as Shape Parameter, Weibull Scope, or Threshold Parameter. Beta (B) Properties Also known as Scale Parameter or Characteristic Life Paramter. If a1, failure rate increases with time. If a=1, failure rate is constant. Here is an example of the Probability Density with respect to time (x): 0.025 -B 0.020 p=08 0.015 p= 3.8 Probability Density Figure 1: Taken from http://www.engineeredsoftware.comasa/weibull.htm. -2 0.010 0.005 0.000 0 50 150 200 100 i O Weibull Distribution a = 10, p = 0.5 a = 10,3 = 1 O 0,8>0 P(X c) = {f(x) dx = e (3) 4 = B.TO ver) sr(1+3) [p(1+2) a"} Mean u = E(X) = B.1(1+ a Variance o2 = V(X) = B2 Alpha (a) Properties Also known as Shape Parameter, Weibull Scope, or Threshold Parameter. Beta (B) Properties Also known as Scale Parameter or Characteristic Life Paramter. If a1, failure rate increases with time. If a=1, failure rate is constant. Here is an example of the Probability Density with respect to time (x): 0.025 -B 0.020 p=08 0.015 p= 3.8 Probability Density Figure 1: Taken from http://www.engineeredsoftware.comasa/weibull.htm. -2 0.010 0.005 0.000 0 50 150 200 100 i O Weibull Distribution a = 10, p = 0.5 a = 10,3 = 1 O