use Excel’s solver function to solve the question

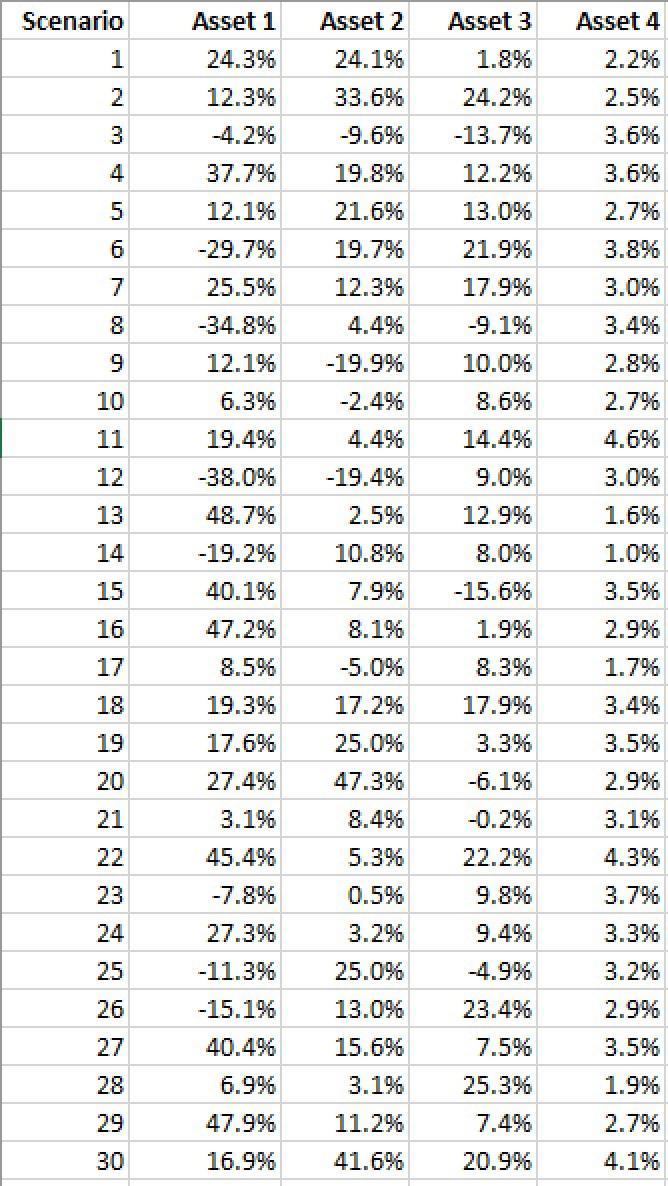
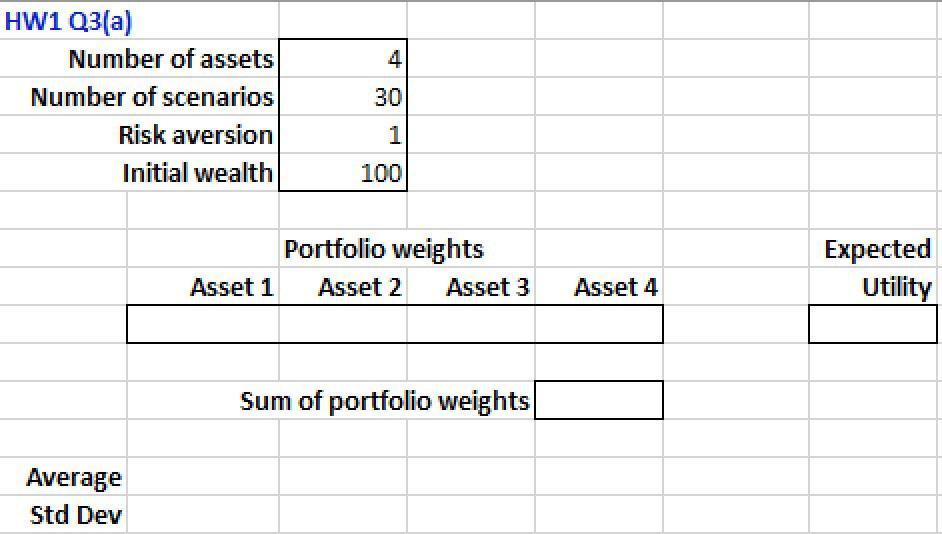
3. (Wealth management) An investor is constructing a portfolio that consists of four assets. Let us denote by x = (x,...,x4) a vector of portfolio weights such that 1x;= 1. The investor is endowed with an initial wealth Wo= 100. The scenarios, or outcomes, are indexed i = 1,..., 30. In scenario i, the return of asset j is rij, so the final wealth in this scenario is W(i) = Wo Ex(1+rij). j=1 Given final wealth W (i), the investor obtains utility u(W (i)) (to be specified below). The goal of the investor is to find the optimal weights of the assets to maximize the expected utility: u(W (i)). 4 Use the data in the worksheet HW1_Q3 of the file HW1.xlsx and the Solver add-in can be used for the parts below. The data in the spreadsheet corresponds to four assets and thirty scenarios. (a) Suppose that the investor's utility is simply equal to the wealth; that is, u(w) = w. In this case, the investor solves the following optimization problem: max X 30 w(i) i=1 4 subject to W (i) = Woxj (1+rij) j=1 max X 4 x; =1, x > 0 j=1 Discuss whether this is a linear model or a non-linear model. Find the optimal portfolio weights and record the corresponding expected utility, the average portfolio return, and the standard deviation of the portfolio return. (b) Suppose that the investor's utility is u(w)=-w-25/25. This means that the investor is significantly risk-averse; that is, the investor is sensitive to losses than to gains. In this case, the investor solves the following optimization problem: 30 -(w (i))^25/25 i=1 subject to W (i) = Wo x, (1 + rij) j=1 xj = 1, x>0 j=1 Discuss whether this is a linear model or a non-linear model. Repeat the analysis in part (a). Hint: The Solver can fail with "poorly scaled" problems. One way to avoid this is to replace the objective function by an equivalent objective function which is better scaled. The basic idea is that maximizing f(x) is equivalent to maximizing 1000f(x), f(x) +500, ef(x) or ln(f(x)) (if f(x) > 0). With the right choice you should not have to change any Solver settings to get optimal solutions.