Question: Use linear approximation, i.e. the tangent line, to approximate 1/ 16.1 as follows: Let at) 2 . Find the equation of the tangent line to

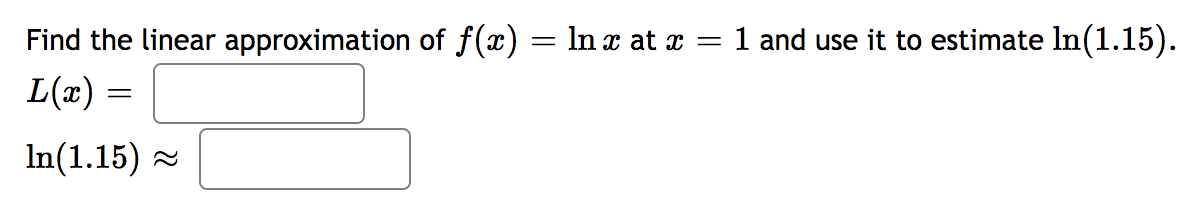
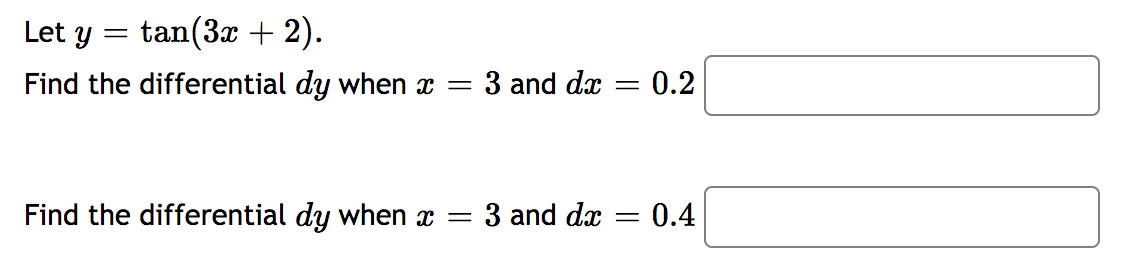
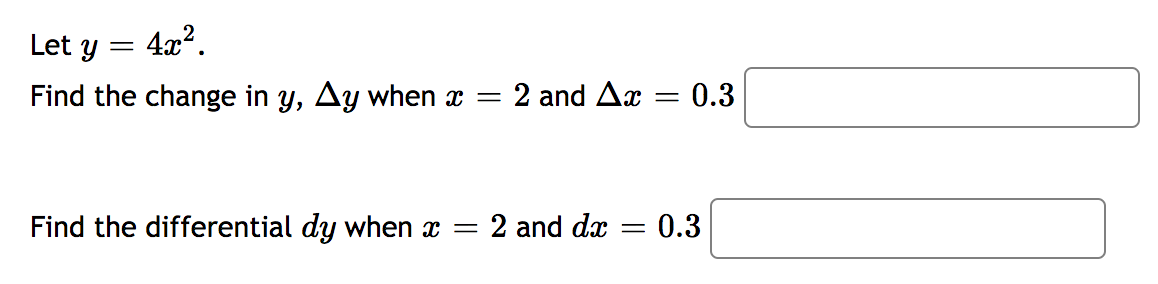
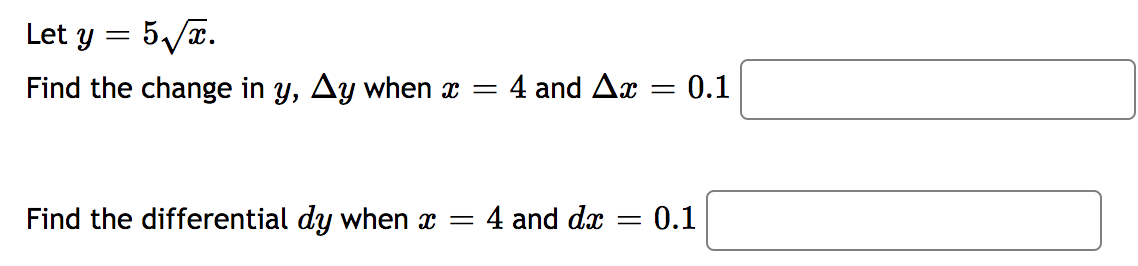
Use linear approximation, i.e. the tangent line, to approximate 1/ 16.1 as follows: Let at) 2 . Find the equation of the tangent line to at) at m = 16 L0\") = Using this, we find our approximation for 16.1 is NOTE: For this part, give your answer to at least 9 significant figures or use an expression to give the exact answer. 1 . 2 as follows: Let f(m) = E and find 1 1.002 Use linear approximation, i.e. the tangent line, to approximate the equation of the tangent line to at) at a "nice" point near 1.002. Then use this to approximate Find the linear approximation of f(x) = Inx at x = 1 and use it to estimate In(1.15). L(ac) = In(1.15) ~The circumference of a sphere was measured to be 89 cm with a possible error of 0.5 cm. Use linear approximation to estimate the maximum error in the calculated surface area. :] Estimate the relative error in the calculated surface area. :] \fLet y = 4x2. Find the change in y, Ay when x = 2 and Ax = 0.3 Find the differential dy when x = 2 and dx = 0.3Let y = 5 x. Find the change in y, Ay when x = 4 and Ax = 0.1 Find the differential dy when x = 4 and dx = 0.1Find the differental of: y = - 2x" + 8x 9 dy =9 .x Find the differential of: y = - 3e dy =Find the differential of: y = 6 sin(8 . x dy=

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

\fLet A be the area of a circle with radius r. If dr dA = 5, find dt when r = 2. dtl_J A spherical snowball is melting in such a way that its radius is decreasing at a rate of 0.4 cm/ min. At what...

0 Question 10 v Suppose a company's revenue function is given by R(q) = q3 -l- 250132 and its cost function is given by C(q) = 320 + 10g, where q is hundreds of units sold/produced, while R(q) and...

. Question 2 > Textbook @ Videos ' [+] Use linear approximation, i.e. the tangent line, to approximate v 64.3 as follows: Let f(a) = vac. Find the equation of the tangent line to f(x) at x = 64 L(ac)...

Use linear approximation, i.e. the tangent line, to approximate 1 0.102 as follows: Let f(ac) = and find the equation of the tangent line to f(x) at a "nice" point near 0.102. Then use this to...

Use linear approximation, i.e. the tangent line, to approximate v 64.3 as follows: Let f(x) = C. Find the equation of the tangent line to f(@) at x = 64 L(x) Using this, we find our approximation for...

~ _ '-r v f v v -w-' Suppose f(2.3) = 5.4 and f'(2.3) = 8 To approximate f(2.5) we need h = and mm is approximately equal to = Enter your answer as a whole number (like -4, 0, or 253) or as a decimal...

Use Linear approximation, i.e. the tangent line, to approximate v" 25.2 as follows: Let x) 2 J}. Find the equation of the tangent line to x] at m = 25 L{:-:) = |: :| Using this, we find our...

M= B= Use linear approximation, i.e. the tangent line, to approximate v 25.2 as follows: Let f(ac) = Vac. The equation of the tangent line in slope-intercept form to f(x) at x - 25 can be written in...

Please need an answer asap Use linear approximation, i.e. the tangent line, to approximate v 49.1 as follows: Let f(x) = VI. The equation of the tangent line in slope-intercept form to f(z) at z - 49...

Use linear approximation, i.e. the tangent line, to approximate v 64.3 as follows: Let f(ac) = Va. The equation of the tangent line in slope-intercept form to f(x ) at x = 64 can be written in the...

Dyna Ltd has acquired land in a business combination. The land is currently developed for industrial use as a site for a factory. The current use of land is presumed to be its highest and vest use...

Temporary hardness of water is due to the presence of : A) Chlorides od Ca and Mg B) Bicarbonates of Ca and Mg C) Sulphates of Ca and Mg D) Nitrates of Ca and Mg

Which one of the following best describes a non - current asset? An asset _ _ _ _ _ _ _ _ _ _ : Question 1 3 Answer a . that has a physical substance b . is physically fixed, like a building c . that...

Case Study After prospering for more than 100 years, General Electric found itself in trouble in the early 2000s, facing the double wallop of a depressed energy sector and the financial crisis of...

5. Get a third party to mediate, so that both parties have the opportunity to go back to their original negotiating point that they had before the third party put forward his/her proposal.

1. Discuss the following statements: a) What we seek to achieve is different from why we seek to achieve it. b) Thoughts are different from what we are thinking about. c) Writing to find out what one...

2. Provide new information and before 20 seconds have elapsed, add more infor-mation. The initial information will then be lost from memory for most people.