USE LINGO. DO NOT USE EXCEL. please show alll workings and include algebraic model.answer will be reported if excel is used.

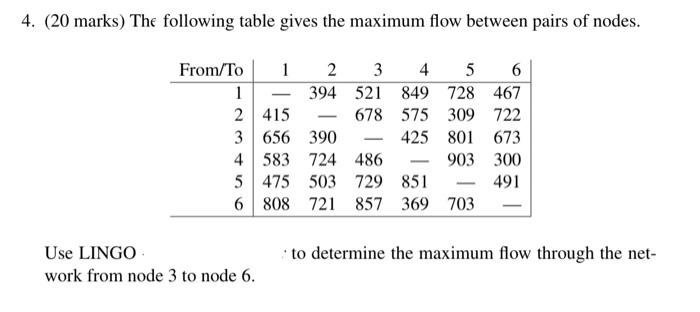
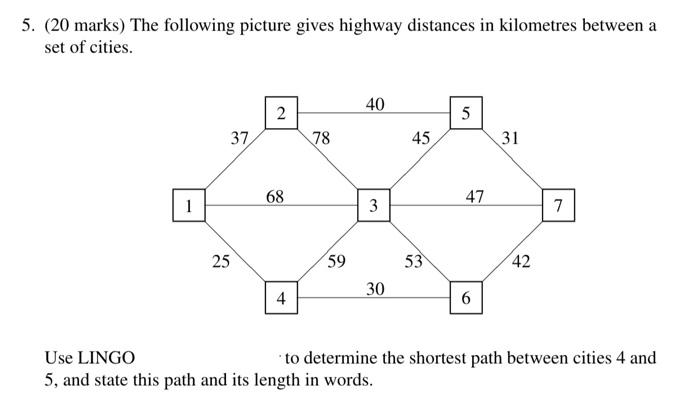
1. (20 marks) A machine shop has six jobs waiting to be done. There are six machines available to do these jobs, and the shop will assign each job to a specific machine. The machines differ in their capabilities, so the times to do each job are different. The following table gives the number of minutes required to do each job, depending on the machine to which it is assigned. Machine Job 1 2 3 4 5 6 1 45 42 48 41 47 51 2 38 34 39 35 36 40 3 56 61 65 59 60 62 4 41 42 39 40 48 43 5 32 28 29 39 36 37 6 42 38 49 43 39 45 (a) The shop wishes to minimize the total number of minutes used to do these jobs. Use LINGO to determine the optimal solution. (b) State this solution so that anyone working in the shop would be able to under- stand it. 2. (a) (15 marks) A company makes calculators at facilities in Shanghai (China), Bonn (Germany), and Cape Town (South Africa). These plants can make 1800, 900, and 2700 calculators per week beyond the demand in the "local" markets of Eastern Asia, Germany, and Africa respectively. All three plants can ship to markets elsewhere: Canada/USA, Latin America, Europe, and Western Asia. The demands per week in these four markets are for 1500, 600, 750, and 2300 calculators per week respectively. Calculators are shipped in boxes of 50. The shipping costs per box are as follows: From/To Canada/USA Latin America Europe Western Asia Shanghai 180 270 205 120 Bonn 230 250 80 190 Cape Town 200 210 185 220 (i) The company wishes to determine how many boxes should be shipped from each of the factories to each of the markets. Solve this model using LINGO (ii) State the solution in words. (b) (10 marks) Now the situation is similar to part (a), but it's also possible to ship between each pair of origins. The cost per box is low because shipments are al- ready being made along these routes and they can take advantage of economies of scale. The costs per box are: From/To Shanghai Bonn Cape Town Shanghai 12 Bonn 13 Cape Town (i) Taking advantage of the transhipment possibilities, re-solve this model using LINGO (ii) State the solution in words. 11 17 14 16 4. (20 marks) The following table gives the maximum flow between pairs of nodes. From/To 1 2 3 4 5 6 1 394 521 849 728 467 2 415 678 575 309 722 3 656 390 425 801 673 4 583 724 486 903 300 5 475 503 729 851 491 6 808 721 857 369 703 Use LINGO work from node 3 to node 6. to determine the maximum flow through the net- 5. (20 marks) The following picture gives highway distances in kilometres between a set of cities. 2 40 5 3 37 78 45 31 68 1 47 3 3 7 25 59 53 42 30 4 6 Use LINGO to determine the shortest path between cities 4 and 5, and state this path and its length in words