Question: Use power series to solve the initial value problem. y' + zy = 0, y(0) = 6, y (0) = 0 hint: after shifting indices,

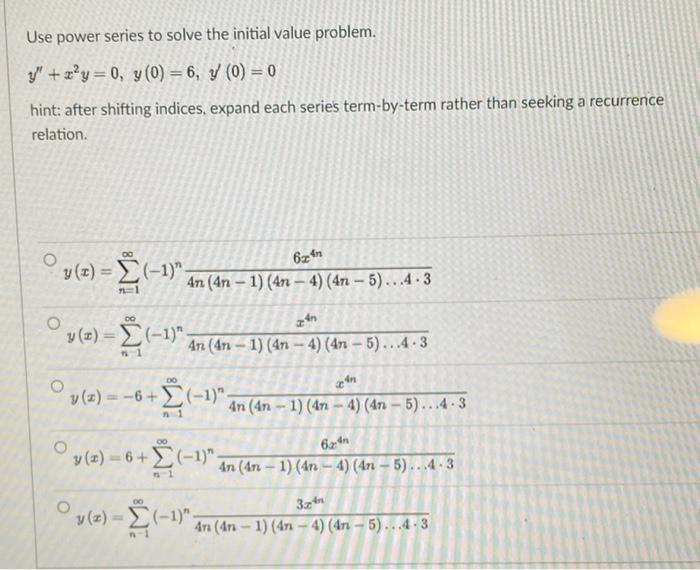
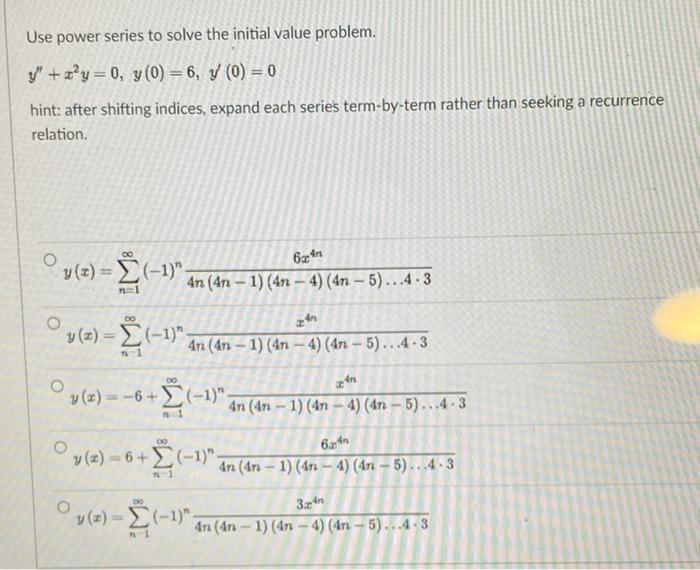
Use power series to solve the initial value problem. y' + zy = 0, y(0) = 6, y (0) = 0 hint: after shifting indices, expand each series term-by-term rather than seeking a recurrence relation. y(z) = (-1) An (An - 1) (47 - 4) (47 - 5) ...4 . 3 -4n O y(z) = Z (-1) An(4n - 1) (47 - 4) (471 - 5) . . . 4 - 3 in y(z) = -6+ 2(-1) An (4n - 1) (47 - 4) (47 - 5) .. .4 . 3 y(z) = 6+ 2 (-1) In (An -1) (4n - 4) (4n - 5) .. .4. 3 1 1 y(z) - Z(-1) An (4n - 1) (471 - 4) (4n - 5). . .4 . 3

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Final Review Set (Summer 2017)- Math 246 Show all your work for each problem 1) [6] (a) Use Euler's Method to approximate the solution to x '(t) = 1+ t sin(tx), x(0) = 0 at t=1 using eight steps. (b)...

Need Help with Computational Physics HW for python on calculating electrostatic potential. Book from Computational physics by mark newman Need it solved in Overrelaxation method: Exercise 9.3: V 0...

1.Use Euler's Method to approximate the solution to at t =1 using eight steps. b) Do the same with the improved Euler method and compare results. 2.Solve the initial value problem 3.Find the general...

1. Solve the given initial value problem. y''- 12y" +52y' - 96y=0; y(0) =1. y'(0)=0, y"(0)=0 y(1)= 2. Find a particular solution to the differential equation using the Method of Undetermined...

y' = ky , to = 0, k has n linearly independent eigenvector insing notation of Section 7.7 in the text D. using a careful proof in a couple of steps to show that P ( t) = I (t) T 10) , and then show...

Please do not use chatgpt to answer _______________________________________________ 1. Which statements are correct A) A block cipher according to Shannon should comprise two atomic operations, i.e....

Reminder: You must show your work to receive full credit on each problem! hint given 1. (a) Use a power series to solve the differential equation y" = y. co and co will be the only unknown in the...

(1) Given IVP y" + 25y =d(t7) + 256(t ), y(0) = 1,y' (0) = 0, Tk (a) Solve the given IVP. Simplify your answers using trigonometric formulas for sin / cos(t). (b) Graph the obtained solution. 8 (2)...

hich statements are correct A block cipher according to Shannon should comprise two atomic operations, i . e . confusion ( obscuring relationship between plaintext and ciphertext ) and diffusion (...

As mentioned in the chapter, the Committee of Sponsoring Organization produced several reports on internal control. One of these relates to internal controls over financial reporting for smaller...

Calculate Laspeyres price indexes for 20112013 from the following data. Use 2005 as the baseyear. Quantity Price Item 2005 2005 2011 2012 2013 21 $0.50 $0.67 $0.68 $0.71 6 1.23 1.85 1.90 191 17 0.84...

Identify and describe an aspect / area / fIdentify and describe an aspect / area / focus of safety that applies or relates to each of the following:ocus of safety that applies or relates to each of...

According to SB 1 0 4 7 , what safety feature must developers of large Al models implement? Multiple Choice Integration with consumer technology standards Enhanced Al creativity and adaptability...

A manufacturing plant has the theoretical capability to produce 162,000 laptops per quarter but currently produces 60,750 units. The conversion cost per quarter is S Ai $7,290,000. There are 40,500...

The following strategic objectives have been derived from a strategy that seeks to improve asset utilization by more careful development and use of its human assets and internal processes: The heart...

Morrison, Inc., has a JIT system in place. Each manufacturing cell is dedicated to the production of a single product or major subassembly. One cell, dedicated to the production of small four...