use provided python code please

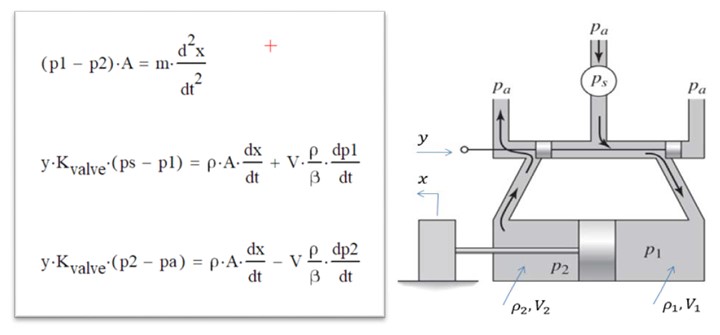
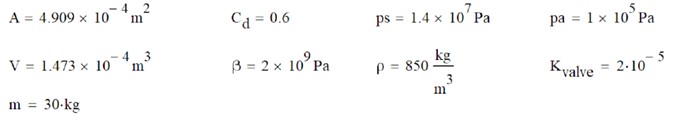
NOTE: All units for the variables and the constants are consistent as given, and no unit conversions of any kind are necessary.

Required:

Use solve_ivp() from scipy.optimize to solve the differential equations for the response to a constant input of y=0.002

The initial conditions are: x=0, x=0, p1=pa, p2=pa

1. From that solution, plot x as a function of time, with nice title and labels.

2. From that solution, plot p1 and p2 together as functions of time, on a new graph, with nice title and labels and legend.

State Variable	Old Name	Derivative
X[0]	x	xdot
X[1]	xdot	xddot=(p1-p2)*A/m
X[2]	p1	p1dot=[yKvalveps-p1-Axdot]/(V))
X[3]	p2	p2dot = -[yKvalve(p2-pa)-Axdot]/(V)

# region imports import numpy as np from scipy.integrate import #JES MISSING CODE import matplotlib.pyplot as plt # endregion # region functions def ode_system(t, X, *params): ''' The ode system is defined in terms of state variables. I have as unknowns: x: position of the piston (This is not strictly needed unless I want to know x(t)) xdot: velocity of the piston p1: pressure on right of piston p2: pressure on left of the piston For initial conditions, we see: x=x0=0, xdot=0, p1=p1_0=p_a, p2=p2_0=p_a :param X: The list of state variables. :param t: The time for this instance of the function. :param params: the list of physical constants for the system. :return: The list of derivatives of the state variables. ''' #unpack the parameters A, Cd, ps, pa, V, beta, rho, Kvalve, m, y=params #state variables #X[0]=x #X[1]=xdot #X[2]=p1 #X[3]=p2 #calculate derivitives #conveniently rename the state variables x = #JES MISSING CODE xdot = #JES MISSING CODE p1 = #JES MISSING CODE p2 = #JES MISSING CODE #use my equations from the assignment xddot = #JES MISSING CODE p1dot = #JES MISSING CODE p2dot = #JES MISSING CODE #return the list of derivatives of the state variables return [#JES MISSING CODE] def main(): #After some trial and error, I found all the action seems to happen in the first 0.02 seconds t=np.linspace(0,0.02,200) #myargs=(A, Cd, Ps, Pa, V, beta, rho, Kvalve, m, y) myargs=(4.909E-4, 0.6, 1.4E7,1.0E5,1.473E-4,2.0E9,850.0,2.0E-5,30, 0.002) #because the solution calls for x, xdot, p1 and p2, I make these the state variables X[0], X[1], X[2], X[3] #ic=[x=0, xdot=0, p1=pa, p2=pa] pa = #JES MISSING CODE ic = #JES MISSING CODE #call odeint with ode_system as callback sln=solve_ivp(#JES MISSING CODE) #unpack result into meaningful names xvals=sln.y[0] xdot=sln.y[1] p1=sln.y[2] p2=sln.y[3] #plot the result plt.subplot(2, 1, 1) plt.subplot(2, 1, 1) plt.plot(t, xvals, 'r-', label='$x$') plt.ylabel('$x$') plt.legend(loc='upper left') ax2=plt.twinx() ax2.plot(t, xdot, 'b-', label='$\dot{x}$') plt.ylabel('$\dot{x}$') plt.legend(loc='lower right') plt.subplot(2,1,2) plt.plot(t, p1, 'b-', label='$P_1$') plt.plot(t, p2, 'r-', label='$P_2$') plt.legend(loc='lower right') plt.xlabel('Time, s') plt.ylabel('$P_1, P_2 (Pa)$') plt.show() # endregion # region function calls if __name__=="__main__": main() # endregion

(p1p2)A=mdt2d2xyKvalve(psp1)=Adtdx+Vdtdp1yKvalve(p2pa)=AdtdxVdtdp2 A=4.909104m2V=1.473104m3m=30kgCd=0.6=2109Paps=1.4107Pa=850m3kgpa=1105PaKvalve=2105