Use Python 3:

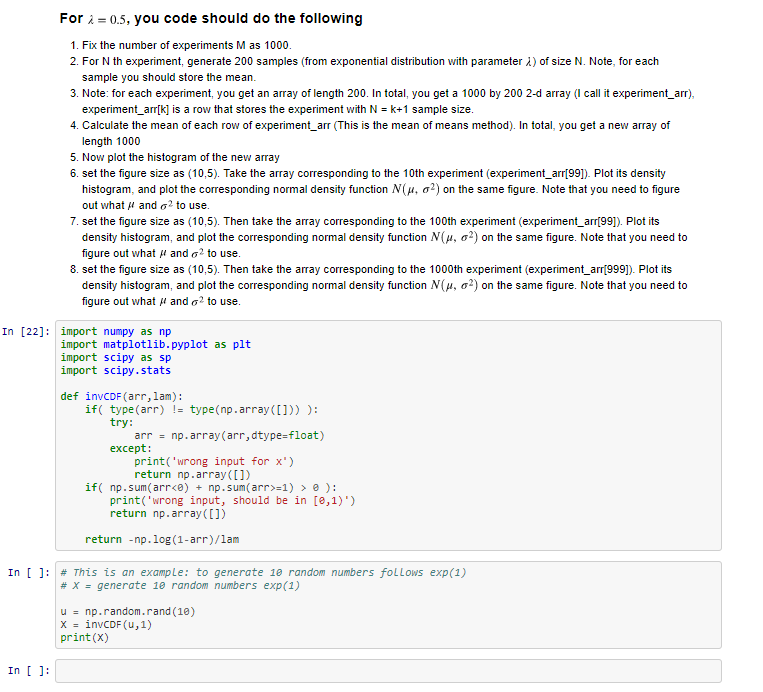
Law of Large Numbers and Central Limit Theorem Keywords: sampling, Law of Large Numbers, Central Limit Theorem we know that the inverse CDF of an exponential distribution with parameter IS Which can be written in python as the following function ## inverse CDF for exponential distribution ## with parameter Lambda-calculation by hand def invcDF (arr,lam): if( != type(np . array([])) ): type (arr) try arr np.array(arr,dtype-float) = except: print('wrong input for x) return np.array(]) if( np.sum (arrke) np.sum(arr>-1)e: print('wrong input, should be in [e,1)') return np.array(]) return -np.log (1-arr) We want to mimic the 'mean of means method' from class to sample from a population of random variables following the exponential distribution with parameter 1. We will do a large set M=1000 of experiments 2. In each experiment, we will obtain 200 samples 3. For the Nh experiment, each sample is of size N. To obtain one sample, this means that you generate N random numbers X^exp(l),i1, 2, ..., N. One sample will be stored as Then you repeat "generating one sample" 200 times, to obtain 200 samples 4. For example A. the first experiment, you will generate 200 samples; each sample is of size 1, which is 1 random number X exp(i), Then you store each sample as In total, you have 200 of them B. the 1000 th experiment, you will generate 200 samples, each sample is of size 1000, which are 1000 random 1000. One sample will be stored as numbers X,-exp(X), i -1, 2, O00 1000 In total, you have 200 of them Law of Large Numbers and Central Limit Theorem Keywords: sampling, Law of Large Numbers, Central Limit Theorem we know that the inverse CDF of an exponential distribution with parameter IS Which can be written in python as the following function ## inverse CDF for exponential distribution ## with parameter Lambda-calculation by hand def invcDF (arr,lam): if( != type(np . array([])) ): type (arr) try arr np.array(arr,dtype-float) = except: print('wrong input for x) return np.array(]) if( np.sum (arrke) np.sum(arr>-1)e: print('wrong input, should be in [e,1)') return np.array(]) return -np.log (1-arr) We want to mimic the 'mean of means method' from class to sample from a population of random variables following the exponential distribution with parameter 1. We will do a large set M=1000 of experiments 2. In each experiment, we will obtain 200 samples 3. For the Nh experiment, each sample is of size N. To obtain one sample, this means that you generate N random numbers X^exp(l),i1, 2, ..., N. One sample will be stored as Then you repeat "generating one sample" 200 times, to obtain 200 samples 4. For example A. the first experiment, you will generate 200 samples; each sample is of size 1, which is 1 random number X exp(i), Then you store each sample as In total, you have 200 of them B. the 1000 th experiment, you will generate 200 samples, each sample is of size 1000, which are 1000 random 1000. One sample will be stored as numbers X,-exp(X), i -1, 2, O00 1000 In total, you have 200 of them