Use simulink to create model

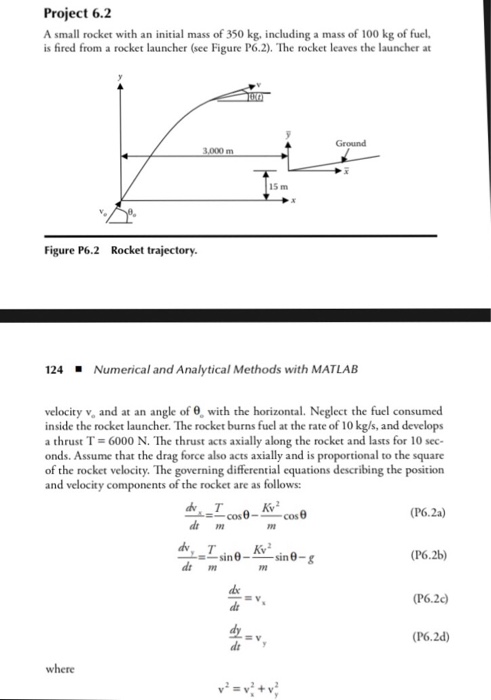
where 0 is the angle the velocity vector makes with the horizontal. m is the mass of the rocket (varies with time). wv, are the x and y components of the rockets velocity relative to the ground. K is the drag coefficient. gis the gravitational constant. (x, y) are the position of the rocket relative to the ground. r is the time of rocket flight. cos =v/v and sin =y/v. Substituting for cos 8 and sin 8 in Equations (P6.2a) and (P6.2b) they become (P6.2e) + V (P6.20) The target lies on ground that has a slope of 5%. The ground elevation,Je relative (P6.2g) PNI to the origin of the coordinate system of the rocket is given by 15+0.05-3000) Numerical Integration of Ordinary Differential Equations125 create a Simulink mode Using Equations (P6.2e). (P6.2. (P6.2c), and (P6.2d) 6Hmttr+that will solve for x, y, vs, and v, forS1 (P6.2g) to solve for y 60 seconds. Use Equation Use a fixed time step of 0.01 second. Take x(0)s 0, y(0)-0, v,0-v,cos ' v,()-v,sin . v.-150 m/s, K 0.045 N-s2/m2, g# 9.81 m/s, .-600, and Print out a table for x,y,%-v,, v, at every 1.0 seconds. Run the program, for 0St S60 seconds (a) (b) Use MATLAB to plot x, andy, vs. and v. v, vs. (c) Assume a linear trajectory between the closest two data points where the rocket hits the ground. The intersection of the two straight lines gives the (x.y) position of where the rocket hits the ground