Use the binomial tree model to value a 4-year 6.5% callable issue with annual payments that is callable in one year at $100 (which means it is not callable at t=0, but it is at t=1 and remains callable until maturity).

What is the value of the call option in t=0?

Use the same binomial tree model to value a 4-year 6.5% putable issue with annual payments, putable in one year at par.(Hint: use Excel's Max function.)

If a 4-year 6.5% callable issue that is callable in one year at $100 is traded at $102.218 in the market, what is the OAS that you need add to all interest rates on the binomial tree, to make the resulting price equal to market price?

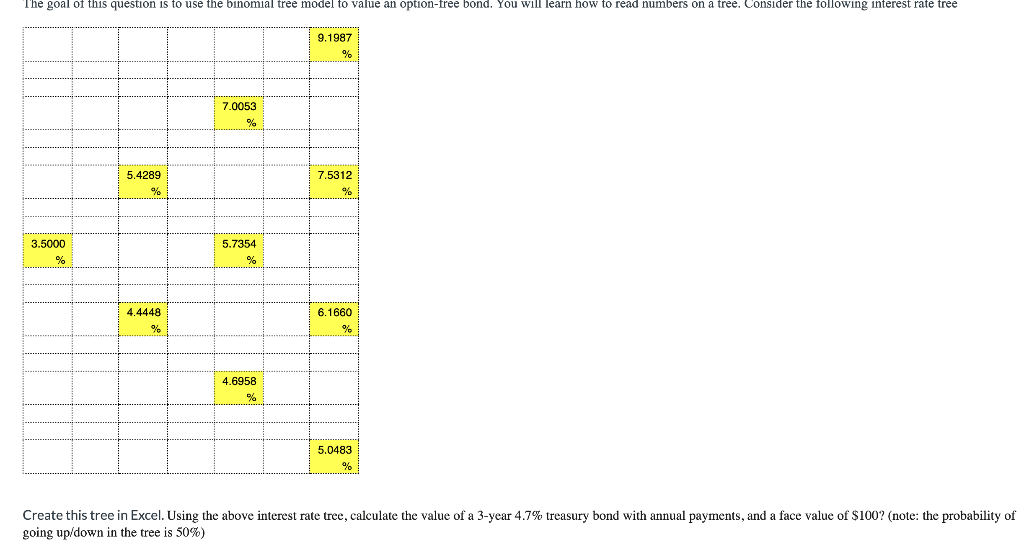
Create this tree in Excel. Using the above interest rate tree, calculate the value of a 3 -year 4.7% treasury bond with annual payments, and a face value of $100 ? (note: the probability of going up/down in the tree is 50% ) Create this tree in Excel. Using the above interest rate tree, calculate the value of a 3 -year 4.7% treasury bond with annual payments, and a face value of $100 ? (note: the probability of going up/down in the tree is 50% )