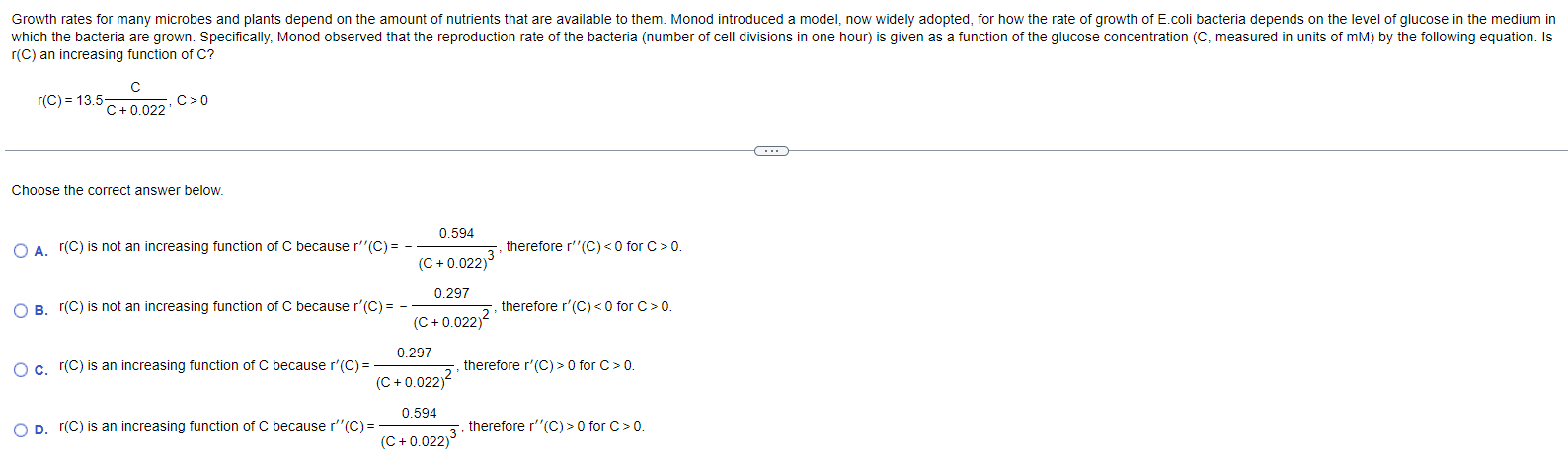
Question: Use the first derivative and the second derivative test to determine where each function is increasing, decreasing, concave up, and concave down. y = -
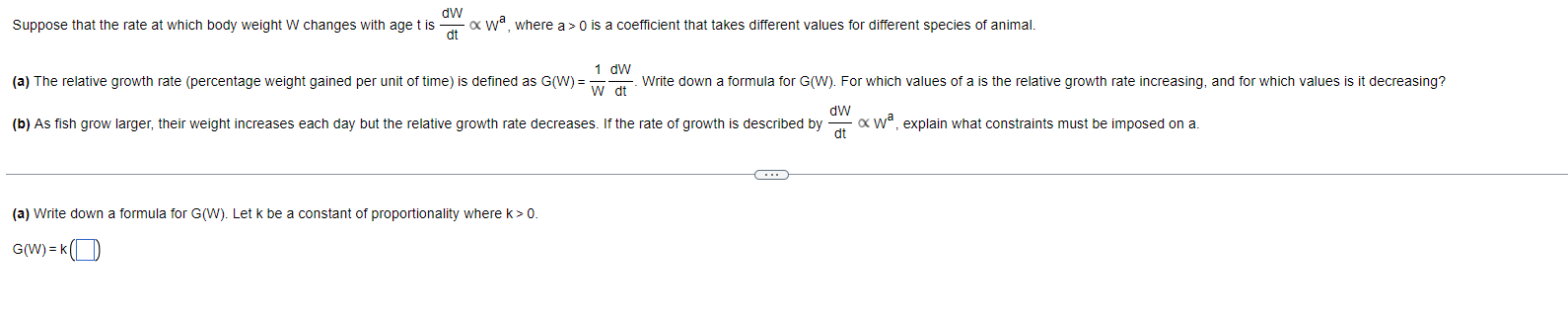








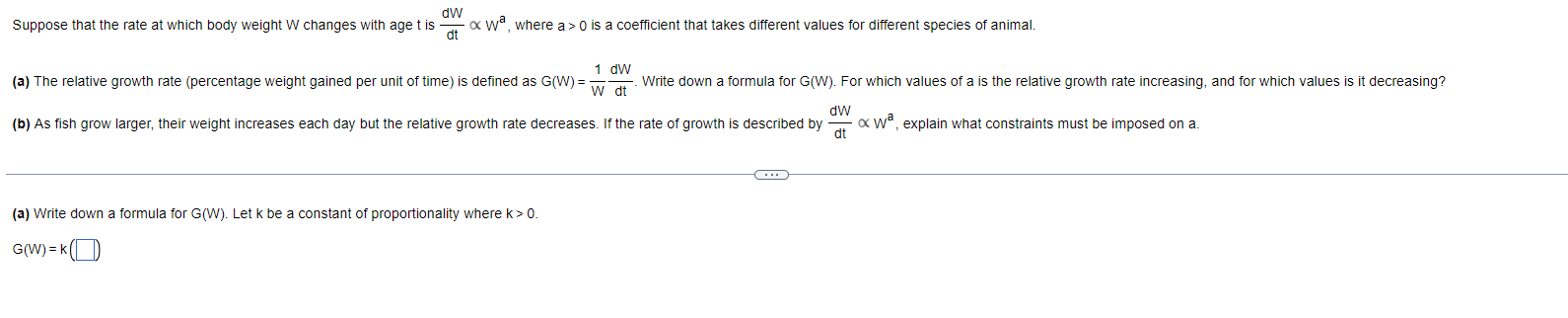





![tunction on [a o] and fta) and rm) have opposite signs the](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6660efc249967_8666660efc237699.jpg)

![= o in [a.t>]. Explain in words why there exists exactly one](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6660efc2cc0d5_8666660efc2bc1d7.jpg)
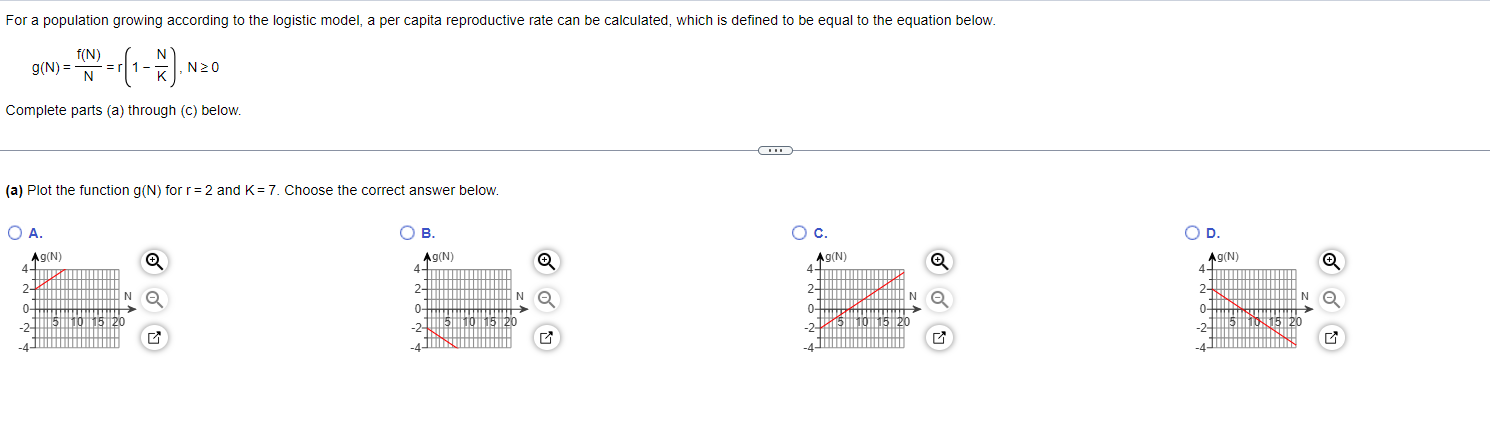
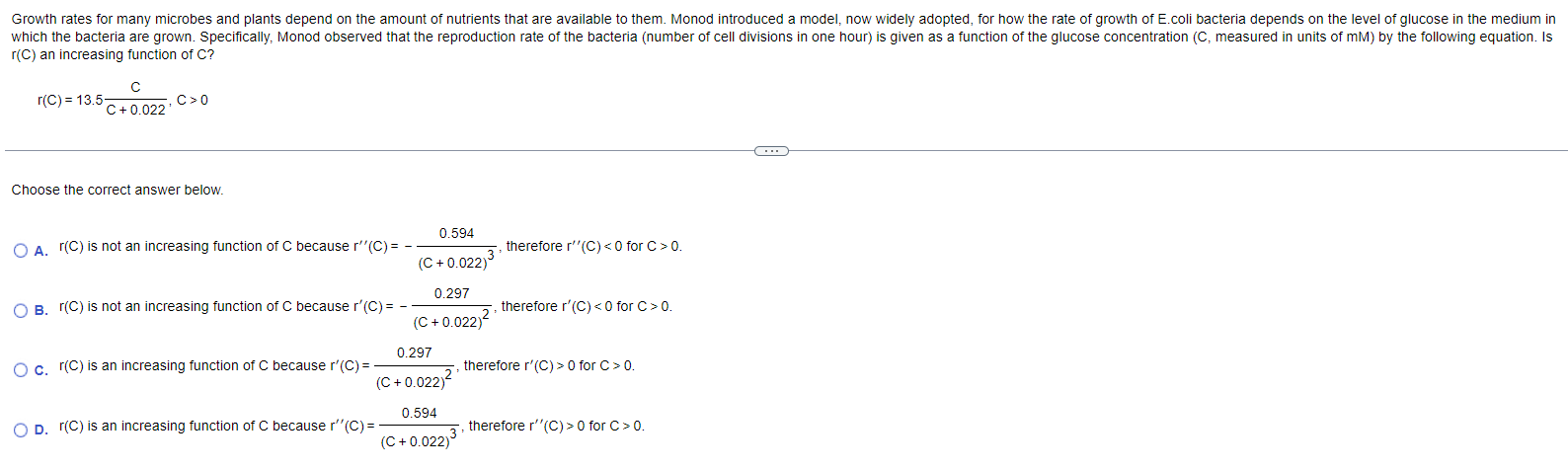
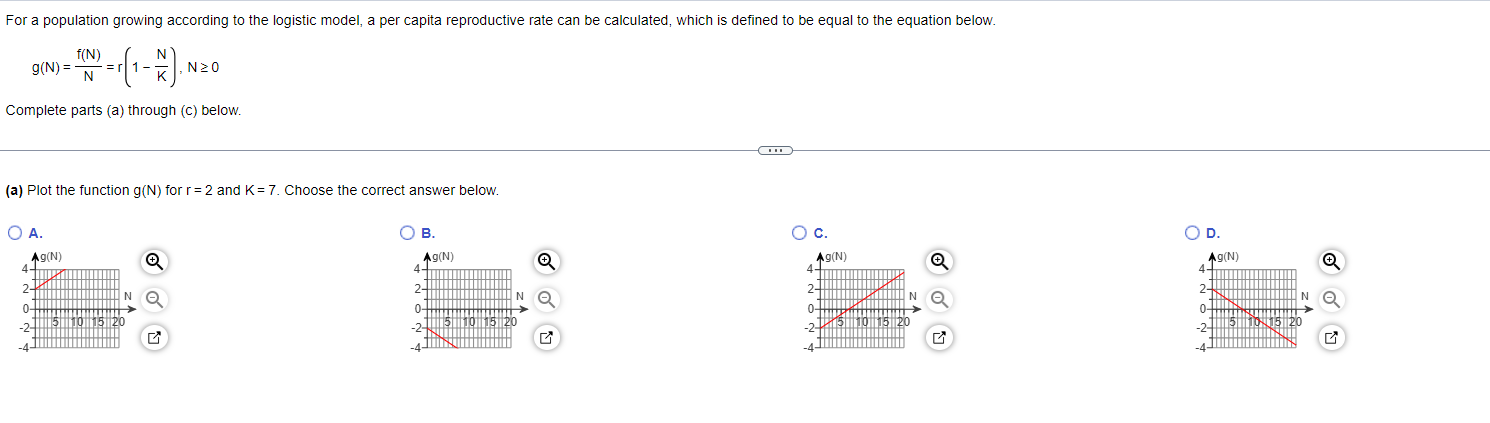
Use the first derivative and the second derivative test to determine where each function is increasing, decreasing, concave up, and concave down. y = - 4x - 5x + 3, XER Use the rst derivative and the second derivative tESt to determine where each function iS Increasing, decreasing: concave up, and concave down. 3 y=x -4X2 +4x+3,xER <:> Use the first derivative test and tile second derivative test to determine where each function is Increasing, decreasing: concave up, and concave down. 5 y=44x+10=x2 Use the first derivative test and the second derivative test to determine where each function is increasing, decreasing, concave up, and concave down. W/ - y = (6x - 1) , XERUse the rst derivative test and the second derivative test to determine where each function is increasing, decreasing: concave up, and concave down. ?x+1 y H ,xyso Use the rst derivative and the second derivative test to determine where each function is increasing, decreasing: concave up, and concave down. y=85in [10(2): osxs1 Use the rst derivative test and the second derivative test to determine where each function is increasing, decreasing: concave up, and concave down. _ x y the = x > 0 E lt is frequently required to solve equations or the form f(x) = 0 When f is a continuous tunction on [a o] and fta) and rm) have opposite signs the intermediateevalue theorem guaranteesthat there exists at least one solution ofthe equation rtx) = o in [a.t>]. Explain in words why there exists exactly one solution in (ab) if in addition. fis differentiable in (an) and f'tx) is either strictly pUSitive or strictly negative throughout (ab) Choose the correct answer below, Q A. The graph of a monotonic function is a parabola that opens upward Ahorizontal line Will intersect the graph at two points, Therefore there exists at least one point cE(a,b) such that [(c) = 0 . The graph of a monotonic function is a horizontal line Given that the function is either strictly positive or strictly negative throughout (a t1) and that [(a) and fill) have opposite signs, there exists at least one point zeta t1) such that We): 0, . The graph of a monotonic function is a parabola that opens downward A horizontal line Wlll intersectthe graph at two points Therefore. there exists at least one paint cetap) such that l(c) : 0. . The graph of a monotonic function is either decreasing or increasing A horizontal line will intersect the graph at only one point, Given that the function is either strictly positive or strictly negative throughout (ab) and that fta) and mu) have opposite signs' there exists cacao) such that ffc) = D
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


