Use the Molecular Dynamics program for a two-dimensional Lennard-Jones system which was as the below to calculate the pair distribution function two different state points. Choose a relatively low density (or a relatively high temperature) state point so that g(r) has a shape similar to that in a dilute gas and a higher density (or a lower temperature) state point with a liquid-like g(r). For each state point you should plot g(r) and, in addition, the dependence of the kinetic, potential and total energy (all per particle) on time. For each state point indicate the initial equilibration period and the part of the trajectory used to calculate the pair correlation function.

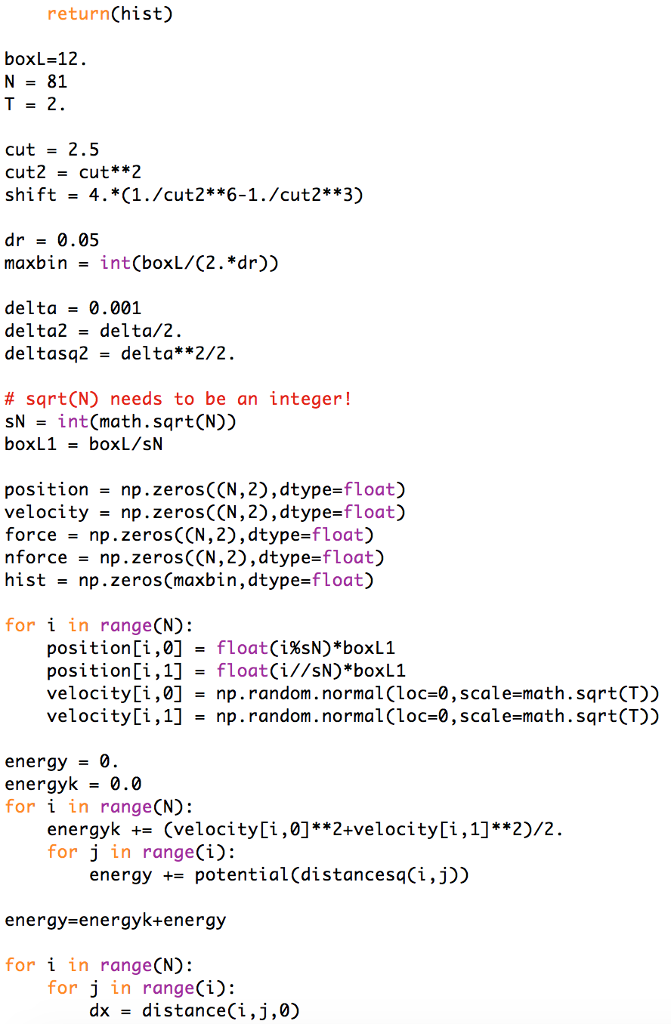
mport numpy as np import math def ff(dx, dy, i): if d2 > cut2 return 0. else: return fff*dx if i == 1: return fff*dy def distance(i,j,k): distancex - position[i,0]-position[j,0] distancex -- boxL*round(distancex/boxL) return distancex ifk== 1: distancey = position [i,1]-position[j,1] distancey -- boxL*round(distancey/boxL) return distancey def potential(d2): if d2 > cut2: return 0 else: return 4.*(di6**2-di6)-shift def distancesq(i,j): distancex position [i ,0]-position [j,0] distancex -- boxL*round(distancex/boxL) distancey = position [1,1]-position [j,1] distancey -- boxL*round(distancey/boxL) return distancex**2+distancey**2 def gr(hist): for i in rangeCN): for j in range(i): bin = round(math. sqrt(distancesq(i,j))/dr) if( bin cut2 return 0. else: return fff*dx if i == 1: return fff*dy def distance(i,j,k): distancex - position[i,0]-position[j,0] distancex -- boxL*round(distancex/boxL) return distancex ifk== 1: distancey = position [i,1]-position[j,1] distancey -- boxL*round(distancey/boxL) return distancey def potential(d2): if d2 > cut2: return 0 else: return 4.*(di6**2-di6)-shift def distancesq(i,j): distancex position [i ,0]-position [j,0] distancex -- boxL*round(distancex/boxL) distancey = position [1,1]-position [j,1] distancey -- boxL*round(distancey/boxL) return distancex**2+distancey**2 def gr(hist): for i in rangeCN): for j in range(i): bin = round(math. sqrt(distancesq(i,j))/dr) if( bin