Use the table

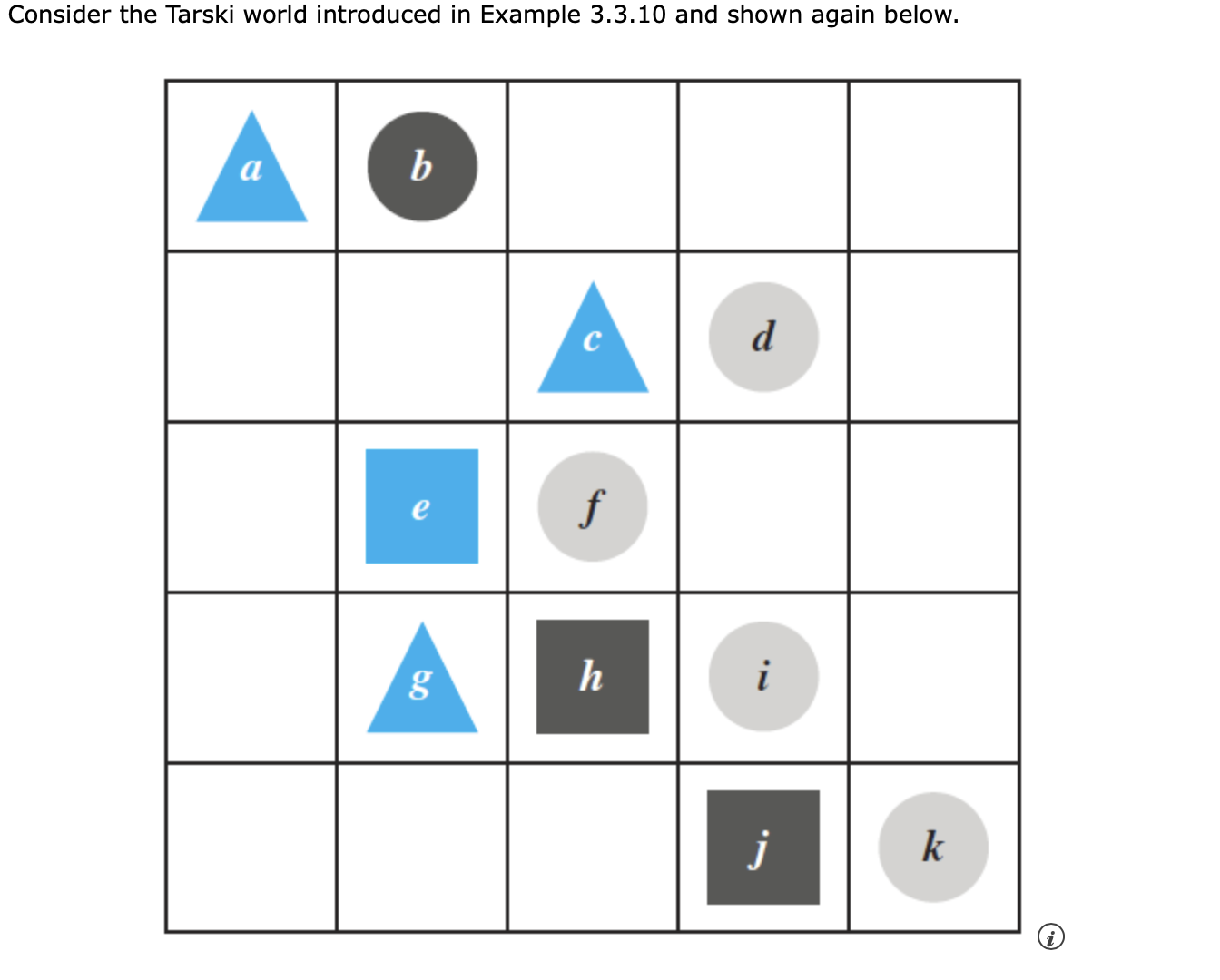
Consider the Tarski world introduced in Example 3.3.10 and shown again below. Parts (b) and (c) refer to the formal logical notation introduced in Example 3.3.10 and shown again below. Formal Logical Notation for a Tarski World (b) Which of the following expresses the given statement using the formal logical notation for a Tarski world? ax(Triangle(x) v (vy(Circle(y) - Above(x, y)))) ax(Triangle(x) A (vy(Circle(y) - Above(y, x)))) vx(Triangle(x) A (3y(Circle(y) - Above(y, x)))) O ax(Triangle(x) A (vy(Circle(y) - Above(x, y)))) O vx(Triangle(x) A (3y(Circle(y) - Above(x, y)))) O ax(Triangle(x) v (vy(Circle(y) - Above(y, x)))) X (c) Which of the following expresses a negation for the given statement using the formal logical notation for a Tarski world? 3x(Triangle(x) A (vy(Circle(y) A ~Above(x, y)))) O vx(~Triangle(x) v (3y(Circle(y) A ~Above(y, x)))) O vx(~Triangle(x) v (3y(Circle(y) A ~Above(x, y)))) O vx(~Triangle(x) v (By(Circle(y) A Below(x, y)))) O ax(Triangle(x) A (vy(Circle(y) A ~Above(y, x)))) O vx(~Triangle(x) v (3y(Circle(y) A Below(y, x))))(3) Consider the following argument. All dogs are carnivorous. Aaron is not a dog. Aaron is not carnivorous. Let C be the set of all carnivorous animals and D the set of all dogs. Does one of the followmg diagrams below show that the argument can have true premises and a false conclusion? If so, choose the diagram; if not, choose "NO." Aaron No. Q) (b) What can you conclude about the validity or invalidity of the following argument form? vx, if P(x) then our). ~P(a) for a particulara. ~Q(a). The argument form is valid. The argument form is invalid. How does the result from part (a) lead to this conclusion? Part (a) shows that it is possible for an argument of the given form to have true premises and a true conclusion. Part (a) shows that it is possible for an argument of the given form to have true premises and a false conclusion. Part (a) shows that it is possible for an argument of the given form to have false premises and a true conclusion. Part (a) shows that it is possible for an argument of the given form to have false premises and a false conclusion